题目内容
2.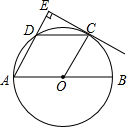 如图所示,AB是⊙O的直径,点C是$\widehat{BD}$的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
如图所示,AB是⊙O的直径,点C是$\widehat{BD}$的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
分析 (1)连接OD,可证明△AOD为等边三角形,可得到∠EAO=∠COB,可证明OC∥AE,可证得结论;
(2)利用△OCD和△AOD都是等边三角形可证得结论.
解答  (1)证明:
(1)证明:
连接OD,如图,
∵C是$\widehat{BD}$的中点,
∴∠BOC=∠COD=60°,
∴∠AOD=60°,且OA=OD,
∴△AOD为等边三角形,
∴∠EAB=∠COB,
∴OC∥AE,
∴∠OCE+∠AEC=180°,
∵CE⊥AE,
∴∠OCE=180°-90°=90°,即OC⊥EC,
∵OC为圆的半径,
∴CE为圆的切线;
(2)解:
四边形AOCD是菱形,理由如下:
由(1)可知△AOD和△COD均为等边三角形,
∴AD=AO=OC=CD,
∴四边形AOCD为菱形.
点评 本题主要考查切线和菱形的判定,掌握切线的判定方法是解题的关键,即有切点时连接圆心和切点,然后证明垂直,没有切点时,过圆心作垂直,证明圆心到直线的距离等于半径.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
10.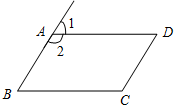 如图,四边形ABCD为平行四边形,延长BA,下列各式不一定成立的是( )
如图,四边形ABCD为平行四边形,延长BA,下列各式不一定成立的是( )
 如图,四边形ABCD为平行四边形,延长BA,下列各式不一定成立的是( )
如图,四边形ABCD为平行四边形,延长BA,下列各式不一定成立的是( )| A. | ∠1+∠2=180° | B. | ∠2+∠B=180° | C. | ∠B+∠C=180° | D. | ∠2+∠C=180° |
 已知△ABC的顶点A、B、C的坐标分别是(-3,0)、(-1,2)、(-2,4).
已知△ABC的顶点A、B、C的坐标分别是(-3,0)、(-1,2)、(-2,4). 如图,在直角坐标系中,四边形OABC的顶点O、A、C的坐标分别是(0,0)、(5,0)、(2,3),当点B的坐标为(7,3)时,四边形OABC是平行四边形.
如图,在直角坐标系中,四边形OABC的顶点O、A、C的坐标分别是(0,0)、(5,0)、(2,3),当点B的坐标为(7,3)时,四边形OABC是平行四边形. 已知,如图1在Rt△ABC中,∠A=90°,AC=AB=2$\sqrt{2}$,D、E分别是AB、AC的中点,若等腰Rt△ABC绕点A逆时针旋转,得到等腰Rt△AB1C1,设旋转角α(0<α<360°),记直线DB1与EC1的交点为P.
已知,如图1在Rt△ABC中,∠A=90°,AC=AB=2$\sqrt{2}$,D、E分别是AB、AC的中点,若等腰Rt△ABC绕点A逆时针旋转,得到等腰Rt△AB1C1,设旋转角α(0<α<360°),记直线DB1与EC1的交点为P. 已知;如图,在四边形ABCD中,点E、F在AC上,且AE=CF,若四边形EBFD是平行四边形.求证:四边形ABCD是平行四边形.
已知;如图,在四边形ABCD中,点E、F在AC上,且AE=CF,若四边形EBFD是平行四边形.求证:四边形ABCD是平行四边形. 如图,AB∥CD,E为AC上一点,∠ABE=∠AEB,∠CDE=∠CED.
如图,AB∥CD,E为AC上一点,∠ABE=∠AEB,∠CDE=∠CED.