题目内容
8.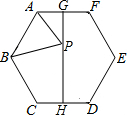 如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )
如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )| A. | 4 | B. | $\sqrt{3}$+2 | C. | $\sqrt{7}$+1 | D. | 2$\sqrt{3}$ |
分析 易知点B关于GH的对称点为点E,连接AE交GH于点P,那么有PB=PE,AP+BP=AE最小.又易知△AEF为等腰三角形,∠AFE=120°,则作FM⊥AE于点M,易求得AM=EM=$\sqrt{3}$,从而AE=2$\sqrt{3}$.
解答 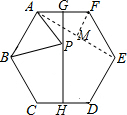 解:利用正多边形的性质可得点B关于GH的对称点为点E,连接AE交GH于点P,那么有PB=PE,AP+BP=AE最小.
解:利用正多边形的性质可得点B关于GH的对称点为点E,连接AE交GH于点P,那么有PB=PE,AP+BP=AE最小.
又易知△AEF为等腰三角形,∠AFE=120°,
则作FM⊥AE于点M,
∵∠AFE=120°,AF=EF,
∴∠FAE=∠FEA=30°,AM=EM,
在RT△AFM中,AF=2,
∴AM=$\frac{\sqrt{3}}{2}$AF=$\sqrt{3}$,
∴AM=EM=$\sqrt{3}$,从而AE=2$\sqrt{3}$,
故AP+BP的最小值为2$\sqrt{3}$.
故选D.
点评 此题主要考查了正多边形的以性质及轴对称最短路线问题,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
3.下列从左到右的变形是因式分解的是( )
| A. | (x-4)(x+4)=x2-16 | B. | x2-y2+2=(x+y)(x-y)+2 | ||
| C. | x2+1=x(x+$\frac{1}{x}$) | D. | a2b+ab2=ab(a+b) |
17.如果a>b,那么下列结论中错误的是( )
| A. | a-1>b-1 | B. | 2a>2b | C. | $\frac{a}{3}$$>\frac{b}{3}$ | D. | -4a>-4b |
18.下表中,y是x的一次函数,写出该函数表达式,并补全下表.
| x | -3 | -2 | -1 | 0 | 1 |
| y | 6 | 4 | 2 | 0 | -2 |
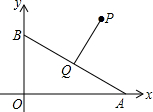 如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.
如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.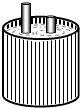 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的$\frac{1}{3}$,另一根露出水面的长度是它的$\frac{1}{5}$,两根铁棒长度之和为220cm,此时木桶中水的深度是80cm.
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的$\frac{1}{3}$,另一根露出水面的长度是它的$\frac{1}{5}$,两根铁棒长度之和为220cm,此时木桶中水的深度是80cm.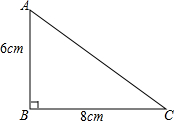 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度沿AB边向点B移动,以此同时,点Q从点C出发,以2cm/s的速度沿CB边向点B移动,如果P,Q同时出发,经过几秒,△PBQ的面积等于8cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度沿AB边向点B移动,以此同时,点Q从点C出发,以2cm/s的速度沿CB边向点B移动,如果P,Q同时出发,经过几秒,△PBQ的面积等于8cm2?