题目内容
19.二次函数y=kx2-6x+7的图象过点(1,2),且与x轴有两个交点A(x1,0),B(x2,0),则x1x2的值是( )| A. | 1 | B. | 3 | C. | 6 | D. | 7 |
分析 可先求得抛物线的解析式,再令y=0可得到一元二次方程,再由根与系数的关系可求得x1x2.
解答 解:
∵二次函数过点(1,2),
∴k-6+7=2,解得k=1,
∴抛物线解析式为y=x2-6x+7,
令y=可得x2-6x+7=0,
由题意可知x1和x2是该方程的两根,
∴x1x2=7,
故选D.
点评 本题主要考查二次函数与x轴的交点,掌握二次函数与x轴交点的横坐标是对应一元二次方程的两根是解题的关键.

练习册系列答案
相关题目
8.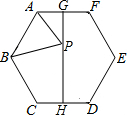 如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )
如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )
 如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )
如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )| A. | 4 | B. | $\sqrt{3}$+2 | C. | $\sqrt{7}$+1 | D. | 2$\sqrt{3}$ |
 如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为8cm2或2$\sqrt{15}$cm2或2$\sqrt{7}$cm2.
如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为8cm2或2$\sqrt{15}$cm2或2$\sqrt{7}$cm2.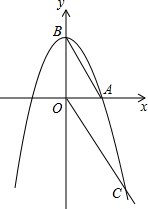 如图,抛物线y1=-x2+a与x轴正半轴交于点A,与y轴交于点B,点C(2,-3)在抛物线y1的图象上,连接AB,OC.
如图,抛物线y1=-x2+a与x轴正半轴交于点A,与y轴交于点B,点C(2,-3)在抛物线y1的图象上,连接AB,OC.
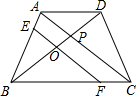 如图,在梯形ABCD中,AD∥BC,BC=2AD,O是BD的中点,过点O作EF∥AC交AB于E,交BC于F,若AC=16cm,求EF的长度.
如图,在梯形ABCD中,AD∥BC,BC=2AD,O是BD的中点,过点O作EF∥AC交AB于E,交BC于F,若AC=16cm,求EF的长度.