题目内容
18.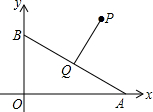 如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.
如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.
分析 由AB=4,点Q是AB的中点,由直角三角形斜边上中线的性质可知OQ=2,然后再求得OP的长,当点O、P、Q在一条直线上时,PQ有最小值.
解答 解:∵在Rt△AOB中,点Q是AB的中点,
∴OQ=$\frac{1}{2}AB=\frac{1}{2}×4=2$.
∵点P的坐标为(4,3),
∴OP=$\sqrt{{4}^{2}+{3}^{2}}$=5.
当点O、Q、P在一条直线上时,PQ最短,
PQ=PO-OQ=5-2=3.
故答案为:3.
点评 本题主要考查的是直角三角形斜边上中线的性质的应用,利用直角三角形斜边上中线的性质求得OP的长是解题的关键.

练习册系列答案
相关题目
13.下列计算,正确的是( )
| A. | (-$\sqrt{3}$)2=-3 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | (2$\sqrt{6}$)2=24 | D. | $\sqrt{(π-3.2)^{2}}$=π-3.2 |
8.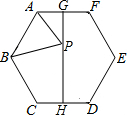 如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )
如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )
 如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )
如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )| A. | 4 | B. | $\sqrt{3}$+2 | C. | $\sqrt{7}$+1 | D. | 2$\sqrt{3}$ |
 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点. 如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为8cm2或2$\sqrt{15}$cm2或2$\sqrt{7}$cm2.
如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为8cm2或2$\sqrt{15}$cm2或2$\sqrt{7}$cm2. 如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为2$\sqrt{3}$.
如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为2$\sqrt{3}$.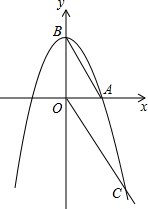 如图,抛物线y1=-x2+a与x轴正半轴交于点A,与y轴交于点B,点C(2,-3)在抛物线y1的图象上,连接AB,OC.
如图,抛物线y1=-x2+a与x轴正半轴交于点A,与y轴交于点B,点C(2,-3)在抛物线y1的图象上,连接AB,OC.