题目内容
3．下列从左到右的变形是因式分解的是（ ）| A． | （x-4）（x+4）=x2-16 | B． | x2-y2+2=（x+y）（x-y）+2 | ||
| C． | x2+1=x（x+$\frac{1}{x}$） | D． | a2b+ab2=ab（a+b） |
分析 分解因式就是把一个多项式化为几个整式的积的形式．因此，要确定从左到右的变形中是否为分解因式，只需根据定义来确定
解答 解：A、B结果不是积的形式，因而不是因式分解，C中$\frac{1}{x}$不是整式，因而不是因式分解，
满足定义的只有D．
故选：D
点评 本题考查的是因式分解的意义，掌握因式分解概念：把一个多项式化为几个整式的积的形式是解题的关键．
练习册系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
13．下列计算，正确的是（ ）
| A． | （-$\sqrt{3}$）2=-3 | B． | $\sqrt{（-3）^{2}}$=-3 | C． | （2$\sqrt{6}$）2=24 | D． | $\sqrt{（π-3.2）^{2}}$=π-3.2 |
8．
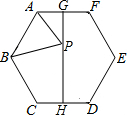如图，已知正六边形ABCDEF的边长为2，G，H分别是AF和CD的中点，P是GH上的动点，连接AP，BP，则AP+BP的最小值为（ ）
如图，已知正六边形ABCDEF的边长为2，G，H分别是AF和CD的中点，P是GH上的动点，连接AP，BP，则AP+BP的最小值为（ ）| A． | 4 | B． | $\sqrt{3}$+2 | C． | $\sqrt{7}$+1 | D． | 2$\sqrt{3}$ |
15．函数$\frac{1}{2}$≤x≤2时，$\frac{1}{4}$≤y≤1，则这个函数可以是（ ）
| A． | y=$\frac{1}{2x}$ | B． | y=$\frac{2}{x}$ | C． | y=$\frac{1}{8x}$ | D． | y=$\frac{8}{x}$ |
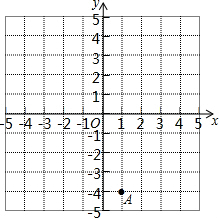如图，在平面直角坐标系内，已知点A的位置；点B的坐标为（3，3）；点C的坐标为（5，1）．
如图，AB∥CD，E、F分别在AB、CD上，若∠1+∠D=180°，那么EF与BD平行吗？为什么？