题目内容
6.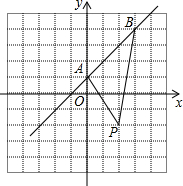 已知:一次函数y=kx+b的图象经过点A(0,1)和B(3,4)两点.
已知:一次函数y=kx+b的图象经过点A(0,1)和B(3,4)两点.(1)求该一次函数的解析式;
(2)若有点P(2,-2),求△ABP的面积;
(3)在(2)的条件下,若直线x=1上有点Q,且S△ABP=S△ABQ,求点Q的坐标.(请直接写出答案)
分析 (1)先把已知点A(0,1)和B(3,4)两点分别代入一次函数解析式求出k,b的值,进而求出函数的解析式;
(2)根据S△ABP=S梯形BHMP-S△AHB-S△AMP即可求得;
(3)分两种情况分别讨论求得.
解答 解:(1)把A(0,1)和B(3,4)两点分别代入函数解析式得:$\left\{\begin{array}{l}{b=1}\\{3k+b=4}\end{array}\right.$.
解得:$\left\{\begin{array}{l}{b=1}\\{k=1}\end{array}\right.$.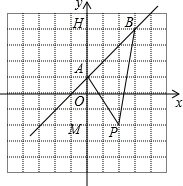
故函数的解析式为:y=x+1;
(2)过B点作BH⊥y轴,过P点作PM⊥y轴,则OH=4,BH=3,OM=PM=2,
S△ABP=S梯形BHMP-S△AHB-S△AMP
=$\frac{1}{2}$(3+2)×6-$\frac{1}{2}$×3×3-$\frac{1}{2}$×3×2
=7.5;
(3)∵S△ABP=S△ABQ,
∴P、Q到AB的距离相等,
①在AB同侧时,PQ∥AB,
∴直线PQ的斜率为1,设为y=x+n
∵P(2,-2),
∴-2=2+n.
∴n=4,
∴直线PQ为y=x-4,
代入x=1得,y=-3,
∴Q(1,-3);
②在AB两侧时,由①可知①的PQ是直线AB向下平移5个单位得到,故,此时AB向上平移5个单位得到Q所在的直线,为y=x+6,
代入x=1得y=7,
∴Q(1,7),
故Q点的坐标为(1,-3)或(1,7).
点评 本题考查的是用待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,比较简单.求三角形的面积时要先画出图形,利用数形结合解答.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | 3m4÷m3=3m2 | B. | m+m2=m3 | C. | (m+n)(m-n)=m2-n2 | D. | ($\frac{m}{2}$)3=$\frac{{m}^{3}}{2}$ |
 如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=4,则k的值为24+8$\sqrt{5}$.
如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=4,则k的值为24+8$\sqrt{5}$.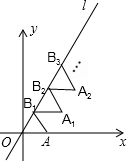 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2016的坐标是(1009,1008$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2016的坐标是(1009,1008$\sqrt{3}$).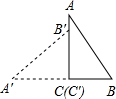 如图,将一块斜边长为15cm,∠B=60°的直角三角板ABC,绕点C逆时针方向旋转90°至△A′B′C′的位置,再沿B′刚好落在斜边AB上,则此三角板向右平移的距离为$\frac{15}{2}$-$\frac{15\sqrt{3}}{2}$.
如图,将一块斜边长为15cm,∠B=60°的直角三角板ABC,绕点C逆时针方向旋转90°至△A′B′C′的位置,再沿B′刚好落在斜边AB上,则此三角板向右平移的距离为$\frac{15}{2}$-$\frac{15\sqrt{3}}{2}$.