题目内容
14. 如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=4,则k的值为24+8$\sqrt{5}$.
如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=4,则k的值为24+8$\sqrt{5}$.
分析 设正方形ODEF的边长为a,则E(a,a),B(4,a+4),再代入反比例函数y=$\frac{k}{x}$求出k的值即可.
解答 解:设正方形ODEF的边长为a,则E(a,a),B(4,a+4),
∵点B、E均在反比例函数y=$\frac{k}{x}$的图象上,
∴$\left\{\begin{array}{l}a=\frac{k}{a}\\ a+4=\frac{k}{4}\end{array}\right.$,解得a=2+2$\sqrt{5}$或a=2-2$\sqrt{5}$(舍去).
当a=2+2$\sqrt{5}$时,k=a2=(2+2$\sqrt{5}$)2=24+8$\sqrt{5}$.
故答案为:24+8$\sqrt{5}$.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
4.由中国发起创立的“亚洲基础设施投资银行”的法定资本金为100 000 000 000美元,用科学记数法表示为( )
| A. | 1.0×109美元 | B. | 1.0×1010美元 | C. | 1.0×1011美元 | D. | 1.0×1012美元 |
 如图,三个小正方形的边长都为4,则图中阴影部分面积的和是6π.(结果保留π)
如图,三个小正方形的边长都为4,则图中阴影部分面积的和是6π.(结果保留π)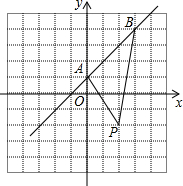 已知:一次函数y=kx+b的图象经过点A(0,1)和B(3,4)两点.
已知:一次函数y=kx+b的图象经过点A(0,1)和B(3,4)两点.