题目内容
1.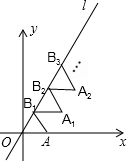 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2016的坐标是(1009,1008$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2016的坐标是(1009,1008$\sqrt{3}$).
分析 根据题意得出直线BB1的解析式为:y=$\sqrt{3}$x,进而得出B,B1,B2,B3坐标,进而得出坐标变化规律,进而得出答案.
解答 解:过B1向x轴作垂线B1C,垂足为C,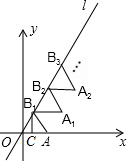
由题意可得:A(1,0),AO∥A1B1,∠B1OC=30°,
∴CB1=OB1cos30°=$\frac{\sqrt{3}}{2}$,
∴B1的横坐标为:$\frac{1}{2}$,则B1的纵坐标为:$\frac{\sqrt{3}}{2}$,
∴点B1,B2,B3,…都在直线y=$\sqrt{3}$x上,
∴B1($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
同理可得出:A的横坐标为:1,
∴y=$\sqrt{3}$,
∴A2(2,$\sqrt{3}$),
…
An(1+$\frac{n}{2}$,$\frac{n\sqrt{3}}{2}$).
∴A2016(1009,1008$\sqrt{3}$),
故答案为:(1009,1008$\sqrt{3}$)
点评 此题主要考查了一次函数图象上点的坐标特征以及数字变化类,得出A点横纵坐标变化规律是解题关键.

练习册系列答案
相关题目
16.移动互联网已全面进入人们的日常生活,截至2016年2月,孝感市4G用户总数达到3820000,数据3820000用科学记数法表示为( )
| A. | 3.8×106 | B. | 3.82×105 | C. | 3.82×106 | D. | 3.82×107 |
11.±3是9的( )
| A. | 平方根 | B. | 相反数 | C. | 绝对值 | D. | 算术平方根 |
 如图,∵∠1=∠2,∴AD∥BC,理由是内错角相等,两直线平行.
如图,∵∠1=∠2,∴AD∥BC,理由是内错角相等,两直线平行.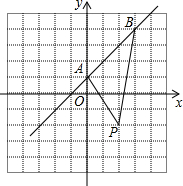 已知:一次函数y=kx+b的图象经过点A(0,1)和B(3,4)两点.
已知:一次函数y=kx+b的图象经过点A(0,1)和B(3,4)两点.