题目内容
6.△ABC中,AB=AC=13,BC=10,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )| A. | $\frac{120}{13}$ | B. | $\frac{120}{13}$或$\frac{60}{13}$ | C. | $\frac{60}{13}$ | D. | 10 |
分析 作AF⊥BC于F,根据等腰三角形三线合一的性质得出BF=CF=$\frac{1}{2}$BC=5,然后根据勾股定理求得AF=12,连接AP,由图可得:S△APB+S△APC=S△ABC,代入数值,解答出即可.
解答 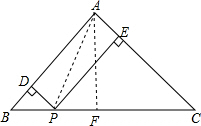 解:作AF⊥BC于F,
解:作AF⊥BC于F,
∵AB=AC,
∴BF=CF=$\frac{1}{2}$BC=5,
∴AF=$\sqrt{1{3}^{2}-{5}^{2}}$=12.
连接AP,
由图可得,S△APB+S△APC=S△ABC,
∵PD⊥AB于D,PE⊥AC于E,AB=AC=13,
∵S△APB+S△APC=S△ABC,
∴$\frac{1}{2}$×13×PD+$\frac{1}{2}$×13×PE=$\frac{1}{2}$×10×12,
∴PD+PE=$\frac{120}{13}$.
故选A.
点评 本题主要考查了等腰三角形的性质,解答时注意,将一个三角形的面积转化成两个三角形的面积和;体现了转化思想.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
5.若一次函数y=(m-3)x+(m+1)(其中m为常数)的图形经过第一、二、四象限,则m的取值范围是( )
| A. | -1≤m≤3 | B. | m<3 | C. | -1<m<3 | D. | m>3 |
6.甲乙两班的学生人数相等,参加了同一次数学测试,两班的平均分分别为$\overline{x}$甲=85分,$\overline{x}$乙=85分,方差分别为S甲2=2.2,S乙2=2.0,那么成绩较为整齐的是( )
| A. | 甲班 | B. | 乙班 | C. | 两班一样整齐 | D. | 无法确定 |
1.若m<n,则下列各式正确的是( )
| A. | $\frac{m}{2}$>$\frac{n}{2}$ | B. | m-2<n-2 | C. | -3m<-3n | D. | -a2m<-a2n |
18.已知x=1+$\sqrt{2}$,y=1-$\sqrt{2}$,则代数式$\sqrt{{x}^{2}+2xy+{y}^{2}}$的值为( )
| A. | 2 | B. | ±2 | C. | 4 | D. | $\sqrt{2}$ |
15.已知一个等腰三角形中有两条边长分别是3cm和4cm,则该三角形的周长是( )
| A. | 10cm | B. | 11cm | C. | 12cm | D. | 10cm或11cm |
 如图,∠1+∠2=230°,b∥c,则∠1、∠2、∠3、∠4各是多少度?
如图,∠1+∠2=230°,b∥c,则∠1、∠2、∠3、∠4各是多少度?