题目内容
1.若m<n,则下列各式正确的是( )| A. | $\frac{m}{2}$>$\frac{n}{2}$ | B. | m-2<n-2 | C. | -3m<-3n | D. | -a2m<-a2n |
分析 根据不等式的性质,分别分析后直接得出答案.
解答 解:A、∵m<n,∴$\frac{m}{2}$<$\frac{n}{2}$,故本选项错误;
B、∵m<n,∴m-2<n-2,故本选项正确;
C、∵m<n,∴-3m>-3n,故本选项错误;
D、∵m<n,∴-a2m≥-a2n,故本选项错误;
故选:B.
点评 此题主要考查了不等式的基本性质.“0”是很特殊的一个数,因此,解答不等式的问题时,应密切关注“0”存在与否,以防掉进“0”的陷阱.不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
相关题目
9. 如图,在⊙O中,直径AB=5,弦BC=3,若点P为弧BC上任意一点,则AP的长不可能为( )
如图,在⊙O中,直径AB=5,弦BC=3,若点P为弧BC上任意一点,则AP的长不可能为( )
 如图,在⊙O中,直径AB=5,弦BC=3,若点P为弧BC上任意一点,则AP的长不可能为( )
如图,在⊙O中,直径AB=5,弦BC=3,若点P为弧BC上任意一点,则AP的长不可能为( )| A. | 3 | B. | 4 | C. | 4.5 | D. | 5 |
16.下列各数中,与8${\;}^{\frac{1}{2}}$-2${\;}^{\frac{1}{2}}$相等的是( )
| A. | 2${\;}^{\frac{1}{2}}$ | B. | 6${\;}^{\frac{1}{2}}$ | C. | 4${\;}^{\frac{1}{2}}$ | D. | 3 |
6.△ABC中,AB=AC=13,BC=10,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
| A. | $\frac{120}{13}$ | B. | $\frac{120}{13}$或$\frac{60}{13}$ | C. | $\frac{60}{13}$ | D. | 10 |
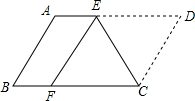 如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.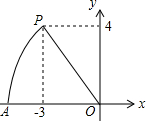 如图,在平面直角坐标系中,点P的坐标为(-3,4),以点O为圆心,以OP长为半径画弧,交x轴的负半轴于点A,则点A的横坐标为( )
如图,在平面直角坐标系中,点P的坐标为(-3,4),以点O为圆心,以OP长为半径画弧,交x轴的负半轴于点A,则点A的横坐标为( )