题目内容
5.若一次函数y=(m-3)x+(m+1)(其中m为常数)的图形经过第一、二、四象限,则m的取值范围是( )| A. | -1≤m≤3 | B. | m<3 | C. | -1<m<3 | D. | m>3 |
分析 根据函数的图形经过第一、二、四象限列出关于m的不等式组,求出m的取值范围即可.
解答 解:∵函数y=(m-3)x+(m+1)(其中m为常数)的图形经过第一、二、四象限,
∴$\left\{\begin{array}{l}m-3<0\\ m+1>0\end{array}\right.$,解得-1<m<3.
故选C.
点评 本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k<0,b>0时函数的图象在一、二、四象限是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.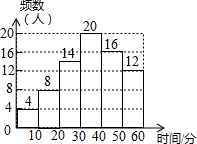 小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.
小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.
①小文同学一共统计了60人
②每天微信阅读不足20分钟的人数有8人
③每天微信阅读30-40分钟的人数最多
④每天微信阅读0-10分钟的人数最少
根据图中信息,上述说法中正确的是( )
 小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.
小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.①小文同学一共统计了60人
②每天微信阅读不足20分钟的人数有8人
③每天微信阅读30-40分钟的人数最多
④每天微信阅读0-10分钟的人数最少
根据图中信息,上述说法中正确的是( )
| A. | ①②③④ | B. | ①②③ | C. | ②③④ | D. | ③④ |
10.一个三角形的两边长分别为2和6,则第三边的长可能为( )
| A. | 4 | B. | 7 | C. | 8 | D. | 10 |
14.下列从左到右的变形,是因式分解的是( )
| A. | (a-b)(a+b)=a2-b2 | B. | x2+2x+3=x(x+2)+3 | C. | ab-a-b+1=(a-1)(b-1) | D. | m2+4m-4=(m-2)2 |
6.△ABC中,AB=AC=13,BC=10,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
| A. | $\frac{120}{13}$ | B. | $\frac{120}{13}$或$\frac{60}{13}$ | C. | $\frac{60}{13}$ | D. | 10 |
 正方形ABCD中,点G为BC上任意一点,DE⊥AG于E,BF∥DE交AG于F.
正方形ABCD中,点G为BC上任意一点,DE⊥AG于E,BF∥DE交AG于F.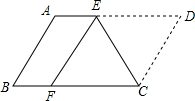 如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.