题目内容
18.已知x=1+$\sqrt{2}$,y=1-$\sqrt{2}$,则代数式$\sqrt{{x}^{2}+2xy+{y}^{2}}$的值为( )| A. | 2 | B. | ±2 | C. | 4 | D. | $\sqrt{2}$ |
分析 根据x=1+$\sqrt{2}$,y=1-$\sqrt{2}$,可以求得x+y的值,从而可以求得$\sqrt{{x}^{2}+2xy+{y}^{2}}$的值.
解答 解:∵x=1+$\sqrt{2}$,y=1-$\sqrt{2}$,
∴x+y=1+$\sqrt{2}$+1-$\sqrt{2}$=2,
∴$\sqrt{{x}^{2}+2xy+{y}^{2}}$=$\sqrt{(x+y)^{2}}=\sqrt{{2}^{2}}=2$,
故选A.
点评 本题考查二次根式的化简求值,解题的关键是明确二次根式化简的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 如图,在⊙O中,直径AB=5,弦BC=3,若点P为弧BC上任意一点,则AP的长不可能为( )
如图,在⊙O中,直径AB=5,弦BC=3,若点P为弧BC上任意一点,则AP的长不可能为( )
 如图,在⊙O中,直径AB=5,弦BC=3,若点P为弧BC上任意一点,则AP的长不可能为( )
如图,在⊙O中,直径AB=5,弦BC=3,若点P为弧BC上任意一点,则AP的长不可能为( )| A. | 3 | B. | 4 | C. | 4.5 | D. | 5 |
6.△ABC中,AB=AC=13,BC=10,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
| A. | $\frac{120}{13}$ | B. | $\frac{120}{13}$或$\frac{60}{13}$ | C. | $\frac{60}{13}$ | D. | 10 |
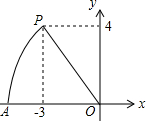 如图,在平面直角坐标系中,点P的坐标为(-3,4),以点O为圆心,以OP长为半径画弧,交x轴的负半轴于点A,则点A的横坐标为( )
如图,在平面直角坐标系中,点P的坐标为(-3,4),以点O为圆心,以OP长为半径画弧,交x轴的负半轴于点A,则点A的横坐标为( ) 如图,一束平行太阳光线照射到正五边形上,则∠1的度数为30°.
如图,一束平行太阳光线照射到正五边形上,则∠1的度数为30°.