题目内容
四边形ABCD中，已知AB＝CD，若再增加一个_________条件（只填写一个）可得四边形ABCD是平行四边形．
AB//CD等
【解析】【解析】
∵在四边形ABCD中，AB=CD，∴可添加的条件是：AB∥CD，∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）．
故答案为：AB//CD．
练习册系列答案
相关题目
已知二次函数的图象经过点（0，﹣3），且顶点坐标为（﹣1，﹣4）．
（1）求该二次函数的解析式；
（2）设该二次函数的图象与x轴的交点为A、B，与y轴的交点为C，求△ABC的面积．
1.【解析】
（1）设，把点代入得：-----------2分
∴函数解析式或-----------------------------2分
2.（2）∵，解得，
∴，，。---------（2分）
∴△ABC的面积=。--------------------------（2分）
【解析】试题分析：（1）先设所求函数解析式是y=a（x+1）2﹣4，再把（0，﹣3）代... 在△ABC中，AB＝8 ㎝，AC＝10 ㎝，P，G，H分别是AB，BC，CA的中点，则四边形APGH的周长是______ ．
18cm
【解析】【解析】
∵P、G、H分别是AB、BC、CA的中点，∴PG、HG为△ABC的中位线，∴AP=AB=×8=4cm，AH=AC=×10=5cm，∴PG∥AC，GH∥AB，∴四边形APGH为平行四边形，HG=AP=4cm，PG=AH=5cm，∴四边形APGH的周长是（4+5）×2=18cm．
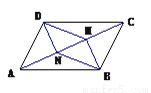
故答案为：18cm． 如图，AC是□ABCD的一条对角线，BM⊥AC， DN⊥AC，垂足分别为M，N，四边形BMDN是平行四边形吗?请选择一种你认为比较好的方法证明．
答案见解析
【解析】试题分析：由四边形ABCD是平行四边形，可得AD=BC，AD∥BC，又由BM⊥AC，DN⊥AC，即可得BM∥DN，∠DNA=∠BMC=90°，然后利用AAS证得△ADN≌△CBM，即可得DN=BM，由有一组对边相等且平行的四边形是平行四边形，即可证得四边形BMDN是平行四边形．
试题解析：【解析】
四边形BMDN是平行四边形．理由如下：
∵四边形ABCD是平... 如图所示，已知AD∥BC，要使四边形ABCD为平行四边形，需要增加的条件是________．(只需填一个你认为正确的条件即可).
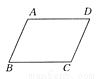
AD＝BC，或AB∥AD(答案不唯一)
【解析】【解析】
根据平行四边形的判定方法，需要增加的条件是：AD=BC或AB∥CD或∠A=∠C或∠B=∠D．故答案为：AD=BC（或AB∥CD）． 以长为5cm， 4cm， 7cm的三条线段中的的两条为边，另一条为对角线画平行四边形，可以画出形状不同的平行四边形的个数是 （ ）
A. 1 B. 2 C. 3 D. 4
C
【解析】【解析】
分别以4cm，5cm为边，7cm为对角线；或以4cm，7cm为边，5cm为对角线；或5cm，7cm为边，4cm为对角线共有三种情况．故选C． 某商店先在广州以每件15元的价格购进某种商品10件，后来又到深圳以每件12.5元的价格购进同种商品40件，如果商店销售这些商品时，每件定价为x元，则会获得不少于12%的利润，用不等式表示以上问题中的不等关系，并把这个不等式变形为“x≥a”或“x≤a”的形式．
x≥14.56.
【解析】试题分析：关系式为：总售价-总进价＞总进价×12%，把相关数值代入化简即可.
试题解析：由题意得
(10＋40)x－(15×10＋12.5×40)≥(15×10＋12.5×40)×12%，
∴x≥14.56. 如图，M，N两点在数轴上表示的数分别是m，n，则下列式子中成立的是（ ）
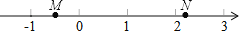
A. m+n＜0 B. 
m＜
n C. |m|
|n|＞0 D. 2+m＜2+n
D
【解析】试题分析：根据M、N两点在数轴上的位置判断出其取值范围，再对各选项进行逐一作出判断：
由M、N两点在数轴上的位置可知：-1＜M＜0，N＞2，
∵-1＜M＜0，N＞2，∴M+N＞0，故A错误.
∵M＜N，∴-M＞-N，故B错误.
∵-1＜M＜0，N＞2，∴|m|-|n|＜0，故C错误．
∵M＜N，∴2+m＜2+n，故D正确.
故选D． 计算：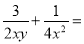 
________．
【解析】试题分析：原式＝
＝．
故答案为： ．