题目内容
如图，M，N两点在数轴上表示的数分别是m，n，则下列式子中成立的是（ ）
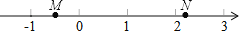
A. m+n＜0 B. 
m＜
n C. |m|
|n|＞0 D. 2+m＜2+n
D
【解析】试题分析：根据M、N两点在数轴上的位置判断出其取值范围，再对各选项进行逐一作出判断：
由M、N两点在数轴上的位置可知：-1＜M＜0，N＞2，
∵-1＜M＜0，N＞2，∴M+N＞0，故A错误.
∵M＜N，∴-M＞-N，故B错误.
∵-1＜M＜0，N＞2，∴|m|-|n|＜0，故C错误．
∵M＜N，∴2+m＜2+n，故D正确.
故选D．
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
地球正面临第六次生物大灭绝，据科学家预测，到2050年，目前的四分之一到一半的物种将会灭绝或濒临灭绝，2012年底，长江江豚数量仅剩约1000头，其数量年平均下降的百分率在13%﹣15%范围内，由此预测，2013年底剩下江豚的数量可能为（ ）头．
A．970 B．860 C．750 D．720
B
【解析】
试题分析：根据2012年底，长江江豚数量仅剩约1000头，其数量年平均下降的百分率在13%﹣15%范围内，得出2013年底剩下江豚的数量的取值范围。设2013年底剩下江豚的数量是x，则列出不等式组解得850﹤x﹤870，符合题意的只有860．
考点一元一次不等式组的应用： 四边形ABCD中，已知AB＝CD，若再增加一个_________条件（只填写一个）可得四边形ABCD是平行四边形．
AB//CD等
【解析】【解析】
∵在四边形ABCD中，AB=CD，∴可添加的条件是：AB∥CD，∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）．
故答案为：AB//CD． 不等式的解集在数轴上表示如图所示，则该不等式可能是___________________.
不唯一，如x－1≤0
【解析】由图形可知，不等式的解集为x≤1.只要所写的不等式的解集为x≤1，即可，答案不唯一. 若a是不等式2x﹣1＞5的解，b不是不等式2x﹣1＞5的解，则下列结论正确的是（ ）
A. a＞b B. a≥b C. a＜b D. a≤b
A
【解析】解2x﹣1＞5得x＞3，．
a是不等式2x﹣1＞5的解则a＞3，b不是不等式2x﹣1＞5的解，则b≤3．
故a＞b．
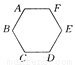
故选A． 如图所示，已知六边形ABCDEF中，∠A＝∠B=∠C＝∠D＝∠E＝∠F＝120°．试说明AB＋BC=EF＋ED．
见解析
【解析】分析：分别延长AB、DC相交于点M，延长AF、DE相交于点N，通过作辅助线我们可以得到∠MBC=∠MCB=60°，再结合三角形内角和定理即可判断△BMC是等边三角形，同理还可以得出△EFN是等边三角形；由“两组对角分别相等的四边形是平行四边形”可知四边形AMDN是平行四边形，从而可以得到AM=DN即可得出结果.
本题解析：分别延长AB、DC相交于点M，延长AF、DE相交... 如图是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM＝4米，AB＝8米，∠MAD＝45°，∠MBC＝30°，则警示牌的高CD为＿米.（结果精确到0.1米，参考数据：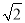 
≈1.41， 
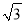≈1.73）
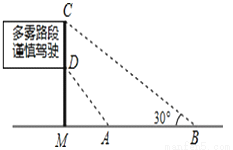
2.9
【解析】试题分析：在Rt△AMD中，∠MAD=45°，AM=4米，可得MD=4米；在Rt△BMC中，BM=AM+AB=12米，∠MBC=30°，可求得MC=4米，所以警示牌的高CD=4-4=2.9米. 已知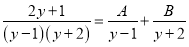
，求A、B的值．
A=1，B=1.
【解析】试题分析：已知等式右边两项通分并利用同分母分式的加法法则计算，利用分式相等的条件即可求出A与B．
试题解析：
【解析】
＝＝＝，
∴，
解得： ． 已知：如图，在?ABCD中，∠ADC，∠DAB的平分线DF，AE分别与线段BC相交于点F，E，DF与AE相交于点G．
（1）求证：AE⊥DF；
（2）若AD＝10，AB＝6，AE＝4，求DF的长．
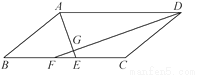
（1）证明见解析；（2）．
【解析】试题分析：（1）根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°，根据角平分线得到∠ADF+∠DAE=（∠ADC+∠DAB）=90°，即可求出结论；
（2）过点D作DH∥AE，交BC的延长线于点H，得到平行四边形AEHD，求出DH=AE=4，EH=AD=10，根据平行四边形的性质和平行线的性质推出DC=FC，AB=EB，求出BF、F...