题目内容
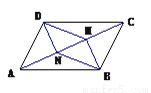
如图，AC是□ABCD的一条对角线，BM⊥AC， DN⊥AC，垂足分别为M，N，四边形BMDN是平行四边形吗?请选择一种你认为比较好的方法证明．
答案见解析
【解析】试题分析：由四边形ABCD是平行四边形，可得AD=BC，AD∥BC，又由BM⊥AC，DN⊥AC，即可得BM∥DN，∠DNA=∠BMC=90°，然后利用AAS证得△ADN≌△CBM，即可得DN=BM，由有一组对边相等且平行的四边形是平行四边形，即可证得四边形BMDN是平行四边形．
试题解析：【解析】
四边形BMDN是平行四边形．理由如下：
∵四边形ABCD是平...
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
已知抛物线的解析式为y=（x-2）2+1，则这条抛物线的顶点坐标是（ ）.
A. （﹣2，1） B. （2，1） C. （2，﹣1） D. （1，2）
B
【解析】根据顶点式y=（x-h）2+k的顶点为（h，k），由y=（x-2）2+1为抛物线的顶点式，顶点坐标为（2，1）．
故选：B． 地球正面临第六次生物大灭绝，据科学家预测，到2050年，目前的四分之一到一半的物种将会灭绝或濒临灭绝，2012年底，长江江豚数量仅剩约1000头，其数量年平均下降的百分率在13%﹣15%范围内，由此预测，2013年底剩下江豚的数量可能为（ ）头．
A．970 B．860 C．750 D．720
B
【解析】
试题分析：根据2012年底，长江江豚数量仅剩约1000头，其数量年平均下降的百分率在13%﹣15%范围内，得出2013年底剩下江豚的数量的取值范围。设2013年底剩下江豚的数量是x，则列出不等式组解得850﹤x﹤870，符合题意的只有860．
考点一元一次不等式组的应用： 已知□ABCD中，∠B=70°，则∠A=______，∠C=______，∠D=______.
110° 110° 70°
【解析】【解析】
由平行四边形的性质得：∠A=180°-∠B=110°，∠C=∠A=70°，∠D=180°-∠B=110°．
故答案为：110°，110°，70°． 在□ABCD中，∠A、∠B的度数之比为5∶4，则∠C等于（ ）
A. 60° B. 80° C. 100° D. 120°
C
【解析】试题分析：解题的关键是熟练掌握平行四边形的邻角互补、对角相等．根据平行四边形的性质可得∠A、∠B互补，从而可求得∠A的度数，即可得到结果．
∵□ABCD，
∴∠A+∠B =180°，
∵∠A、∠B的度数之比为5∶4，
∴∠C =∠A=100°．
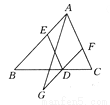
故选C． 如图所示，已知D，E，F分别在△ABC的边BC，AB，AC上，且DE∥AF，DE＝AF，将FD延长至G，使FG＝2DF，连接AG，则ED，AG互相平分吗?请说明理由．
互相平分
【解析】试题分析：求ED与AG互相平分，只要证明四边形AEGD是平行四边形即可解答，由DE∥AC，DE=AF，可得四边形AEDF是平行四边形，所以，AE∥DF且AE=DF，又FG=2DF，则AE=GD，所以，四边形AEGD是平行四边形，即可得出ED与AG互相平分．
试题解析：证明：如图，连接AD，GE，∵DE∥AC，DE=AF，∴四边形AEDF是平行四边形，∴AE∥DF且AE... 四边形ABCD中，已知AB＝CD，若再增加一个_________条件（只填写一个）可得四边形ABCD是平行四边形．
AB//CD等
【解析】【解析】
∵在四边形ABCD中，AB=CD，∴可添加的条件是：AB∥CD，∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）．
故答案为：AB//CD． 不等式的解集在数轴上表示如图所示，则该不等式可能是___________________.
不唯一，如x－1≤0
【解析】由图形可知，不等式的解集为x≤1.只要所写的不等式的解集为x≤1，即可，答案不唯一. 已知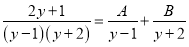
，求A、B的值．
A=1，B=1.
【解析】试题分析：已知等式右边两项通分并利用同分母分式的加法法则计算，利用分式相等的条件即可求出A与B．
试题解析：
【解析】
＝＝＝，
∴，
解得： ．