题目内容
计算：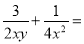 
________．
【解析】试题分析：原式＝
＝．
故答案为： ．
练习册系列答案
相关题目
四边形ABCD中，已知AB＝CD，若再增加一个_________条件（只填写一个）可得四边形ABCD是平行四边形．
AB//CD等
【解析】【解析】
∵在四边形ABCD中，AB=CD，∴可添加的条件是：AB∥CD，∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）．
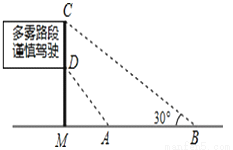
故答案为：AB//CD． 如图是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM＝4米，AB＝8米，∠MAD＝45°，∠MBC＝30°，则警示牌的高CD为＿米.（结果精确到0.1米，参考数据：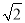 
≈1.41， 
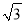≈1.73）
2.9
【解析】试题分析：在Rt△AMD中，∠MAD=45°，AM=4米，可得MD=4米；在Rt△BMC中，BM=AM+AB=12米，∠MBC=30°，可求得MC=4米，所以警示牌的高CD=4-4=2.9米. 已知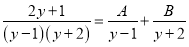
，求A、B的值．
A=1，B=1.
【解析】试题分析：已知等式右边两项通分并利用同分母分式的加法法则计算，利用分式相等的条件即可求出A与B．
试题解析：
【解析】
＝＝＝，
∴，
解得： ． 若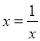
，则分式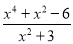
的值为( )
A. 0 B. 1 C. －1 D. －2
C
【解析】试题分析：∵即x2＝1，
＝＝x2－2＝1－2＝－1，
故选C． 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
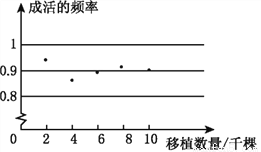
(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
（1）0.9附近，0.9；（2）①4.5，15万棵.
【解析】（1）由图可知，成活概率在0.9上下波动，故可估计这种树苗成活的频率稳定在0.9，成活的概率估计值为0.9；
（2）①5×成活率即为所求的成活的树苗棵树；
②方法1:利用成活率求得需要树苗棵树，减去已移植树苗数即为所求的树苗的棵树；
方法2：设还需移植这种树苗万棵，根据成活率及成活总数列出方程即可。 动物学家通过大量的调查估计，某种动物活到20岁的概率为0.8，活到25岁的概率为0.6，则现年20岁的这种动物活到25岁的概率是（ ）
A. 0.8 B. 0.75 C. 0.6 D. 0.48
B
【解析】设共有这种动物x只，则活到20岁的只数为0.8x,活到25岁的只数为0.6x,故现年20岁到这种动物活到25岁的概率为=0.75,故选B. 已知：如图，在?ABCD中，∠ADC，∠DAB的平分线DF，AE分别与线段BC相交于点F，E，DF与AE相交于点G．
（1）求证：AE⊥DF；
（2）若AD＝10，AB＝6，AE＝4，求DF的长．
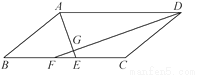
（1）证明见解析；（2）．
【解析】试题分析：（1）根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°，根据角平分线得到∠ADF+∠DAE=（∠ADC+∠DAB）=90°，即可求出结论；
（2）过点D作DH∥AE，交BC的延长线于点H，得到平行四边形AEHD，求出DH=AE=4，EH=AD=10，根据平行四边形的性质和平行线的性质推出DC=FC，AB=EB，求出BF、F... 如图所示，已知在平行四边形ABCD中，BE=DF．求证：AE=CF．
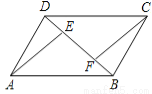
证明：∵BE=DF，
∴BE-EF=DF-EF，
∴DE=BF，
∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∴∠ADE=∠CBF，
在△ADE和△CBF中，
∴△ADE≌△CBF（SAS），
∴AE=CF．
【解析】
求出DE=BF，根据平行四边形性质求出AD=BC，AD∥BC，推出∠ADE=∠CBF，证出△ADE≌△CBF即可．