��Ŀ����
ij�̵����ڹ�����ÿ��15Ԫ�ļ۸�ij����Ʒ10���������ֵ�������ÿ��12.5Ԫ�ļ۸�ͬ����Ʒ40��������̵�������Щ��Ʒʱ��ÿ������ΪxԪ������ò�����12%�������ò���ʽ��ʾ���������еIJ��ȹ�ϵ�������������ʽ����Ϊ��x��a����x��a������ʽ��
 x��14.56.
�������������������ϵʽΪ�����ۼ�-�ܽ��ۣ��ܽ��ۡ�12%���������ֵ���뻯��.
����������������
(10��40)x��(15��10��12.5��40)��(15��10��12.5��40)��12%��
��x��14.56.
x��14.56.
�������������������ϵʽΪ�����ۼ�-�ܽ��ۣ��ܽ��ۡ�12%���������ֵ���뻯��.
����������������
(10��40)x��(15��10��12.5��40)��(15��10��12.5��40)��12%��
��x��14.56.
��ƽ��ֱ������ϵ�У���������y=x2-4������ƽ��2����λ��������ƽ��2����λ���õ��������ߵĽ���ʽ�ǣ� ��
A. y=(x+2)2+2 B. y=(x-2)2-2 C. y=(x-2)2+2 D. y=(x+2)2-2
 B
��������������������ݶ��κ���ͼ������Ҽ����ϼ��¼���ƽ�ƹ��ɣ���֪����y=x2��4����ƽ��2����λ���ã�y=��x��2��2��4��������ƽ��2����λ���ã�y=��x��2��2��2��
��ѡB��
B
��������������������ݶ��κ���ͼ������Ҽ����ϼ��¼���ƽ�ƹ��ɣ���֪����y=x2��4����ƽ��2����λ���ã�y=��x��2��2��4��������ƽ��2����λ���ã�y=��x��2��2��2��
��ѡB�� �ڡ�ABCD�У���A����B�Ķ���֮��Ϊ5��4�����C���ڣ� ��
A. 60�� B. 80�� C. 100�� D. 120��
 C
���������������������Ĺؼ�����������ƽ���ı��ε��ڽǻ������Խ���ȣ�����ƽ���ı��ε����ʿɵá�A����B�������Ӷ�����á�A�Ķ��������ɵõ������
�ߡ�ABCD��
���A+��B =180�㣬
�ߡ�A����B�Ķ���֮��Ϊ5��4��
���C =��A=100�㣮
��ѡC��
C
���������������������Ĺؼ�����������ƽ���ı��ε��ڽǻ������Խ���ȣ�����ƽ���ı��ε����ʿɵá�A����B�������Ӷ�����á�A�Ķ��������ɵõ������
�ߡ�ABCD��
���A+��B =180�㣬
�ߡ�A����B�Ķ���֮��Ϊ5��4��
���C =��A=100�㣮
��ѡC�� �ı���ABCD�У���֪AB��CD����������һ��_________������ֻ��дһ�����ɵ��ı���ABCD��ƽ���ı��Σ�
 AB//CD��
����������������
�����ı���ABCD�У�AB=CD��������ӵ������ǣ�AB��CD�����ı���ABCD��ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ���
�ʴ�Ϊ��AB//CD��
AB//CD��
����������������
�����ı���ABCD�У�AB=CD��������ӵ������ǣ�AB��CD�����ı���ABCD��ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ���
�ʴ�Ϊ��AB//CD�� A��B��C��D��ͬһƽ���ڣ��Ӣ�AB��CD����AB��CD����BC��AD����BC��AD�����ĸ���������ѡ��������ʹ�ı���ABCD��Ϊƽ���ı��ε�ѡ�����У� ��
A. 3�� B 4�� C 5�� D 6��
 B
���������������������һ��Ա�ƽ������ȡ�����Ա߷ֱ�ƽ�С�����Ա߷ֱ�����������ж�.����ȷ��ѡ��Ϊ���٢ۡ��ڢܡ��٢ڡ��ۢ������ж�����.
B
���������������������һ��Ա�ƽ������ȡ�����Ա߷ֱ�ƽ�С�����Ա߷ֱ�����������ж�.����ȷ��ѡ��Ϊ���٢ۡ��ڢܡ��٢ڡ��ۢ������ж�����. ����ʽ�Ľ⼯�������ϱ�ʾ��ͼ��ʾ����ò���ʽ������___________________.

 ��Ψһ����x��1��0
����������ͼ�ο�֪������ʽ�Ľ⼯Ϊx��1.ֻҪ��д�IJ���ʽ�Ľ⼯Ϊx��1�����ɣ��𰸲�Ψһ.
��Ψһ����x��1��0
����������ͼ�ο�֪������ʽ�Ľ⼯Ϊx��1.ֻҪ��д�IJ���ʽ�Ľ⼯Ϊx��1�����ɣ��𰸲�Ψһ. ��a�Dz���ʽ2x��1��5�Ľ⣬b���Dz���ʽ2x��1��5�Ľ⣬�����н�����ȷ���ǣ�������
A. a��b B. a��b C. a��b D. a��b
 A
����������2x��1��5��x��3����
a�Dz���ʽ2x��1��5�Ľ���a��3��b���Dz���ʽ2x��1��5�Ľ⣬��b��3��
��a��b��
��ѡA��
A
����������2x��1��5��x��3����
a�Dz���ʽ2x��1��5�Ľ���a��3��b���Dz���ʽ2x��1��5�Ľ⣬��b��3��
��a��b��
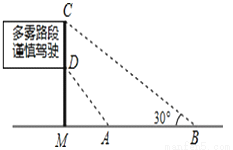
��ѡA�� ��ͼ�Ǵ����ڸ��ٹ�·ˮƽ�����ϵĽ�ͨ��ʾ�ƣ��������õ��������ݣ�AM��4�ף�AB��8�ף���MAD��45�㣬��MBC��30�㣬��ʾ�Ƶĸ�CDΪ����.�������ȷ��0.1�ף��ο����ݣ� 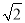 ��1.41��
��1.41�� 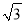 ��1.73��
��1.73��
 2.9
�������������������Rt��AMD�У���MAD=45�㣬AM=4�ף��ɵ�MD=4�ף���Rt��BMC�У�BM=AM+AB=12�ף���MBC=30�㣬�����MC=4�ף����Ծ�ʾ�Ƶĸ�CD=4-4=2.9��.
2.9
�������������������Rt��AMD�У���MAD=45�㣬AM=4�ף��ɵ�MD=4�ף���Rt��BMC�У�BM=AM+AB=12�ף���MBC=30�㣬�����MC=4�ף����Ծ�ʾ�Ƶĸ�CD=4-4=2.9��. ����ѧ��ͨ�������ĵ�����ƣ�ij�ֶ���20��ĸ���Ϊ0.8���25��ĸ���Ϊ0.6��������20������ֶ���25��ĸ����ǣ�������
A. 0.8 B. 0.75 C. 0.6 D. 0.48
 B
���������蹲�����ֶ���xֻ����20���ֻ��Ϊ0.8x,�25���ֻ��Ϊ0.6x,������20�굽���ֶ���25��ĸ���Ϊ=0.75,��ѡB.
B
���������蹲�����ֶ���xֻ����20���ֻ��Ϊ0.8x,�25���ֻ��Ϊ0.6x,������20�굽���ֶ���25��ĸ���Ϊ=0.75,��ѡB. 
