题目内容
18.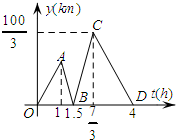 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.(1)求线段OA所在直线的函数表达式;
(2)当20<y<30时,求t的取值范围;
(3)丙骑摩托车与乙同时出发,从N地沿同一条公路匀速前往M地.若丙经过$\frac{4}{3}$h与乙相遇.问丙出发后多少时间与甲相遇?
分析 由图可知甲速度为乙的3倍,即可求得甲乙速度和MN两地距离;
(1)根据乙速度,可以求得点A坐标,即可解题;
(2)设直线BC解析式为y=kt+b,代入B、C点坐标可以求得解析式,即可解题;
(3)根据乙丙相遇时间可以求出丙速度,即可解题.
解答 解:由图可知,甲出发后半小时与乙相遇,此时乙走了1.5小时,
∴甲速度为乙速度的3倍;
设甲速度为3x,乙速度为x,则在$\frac{7}{3}$h时,甲乙相距$\frac{100}{3}$km,此时甲出发($\frac{7}{3}$-1)h=$\frac{4}{3}$h,
可得:3x•$\frac{4}{3}$-$\frac{7}{3}$x=$\frac{100}{3}$,解得:x=20,
∴甲速度为60km/h,乙速度为20km/h,MN两地距离80km;
(1)乙出发1h,甲乙相距20×1=20(km),
∴点A坐标为(1,20),
∴线段OA所在直线的函数表达式为y=20x;
(2)设直线BC解析式为y=kt+b,
代入B、C得:$\left\{\begin{array}{l}{\frac{100}{3}=\frac{7}{3}k+b}\\{0=1.5k+b}\end{array}\right.$,解得:k=40,b=-60,
∴直线BC解析式为y=40t-60,
当y=20时,t=2,当y=30时,t=$\frac{9}{4}$,
∴当20<y<30时,2<t<$\frac{9}{4}$;
(3)乙丙同时出发,$\frac{4}{3}$h后相遇,设丙速度为x,
则$\frac{4}{3}$(20+x)=80,解得:x=40km/h,
设丙出发a小时后,甲丙相遇,
∵甲晚一小时出发,∴40a+60(a-1)=80,
解得:a=$\frac{7}{5}$h,
∴丙出发后$\frac{7}{5}$h与甲相遇;
答:丙出发后$\frac{7}{5}$h与甲相遇.
点评 本题考查了一次函数的实际应用,考查了代入法求一次函数解析式的方法,本题中求得MN距离和甲、乙、丙的速度是解题的关键.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案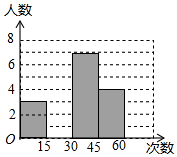 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:| 分 组 | 频数 | 频率 |
| 第一组(0≤x<15) | 3 | 0.15 |
| 第二组(15≤x<30) | a | 0.3 |
| 第三组(30≤x<45) | 7 | 0.35 |
| 第四组(45≤x<60) | 4 | b |
(2)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?
| A. | y=3(x-1)2-1 | B. | y=3(x+1)2-1 | C. | y=3(x-1)2+1 | D. | y=3(x+1)2+1 |
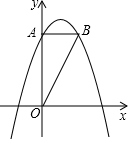 如图,已知抛物线y=ax2+bx+4经过点(2,4),(-2,-2),交y轴于点A,过点A作AB⊥y轴交抛物线于点B.
如图,已知抛物线y=ax2+bx+4经过点(2,4),(-2,-2),交y轴于点A,过点A作AB⊥y轴交抛物线于点B.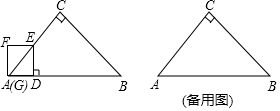
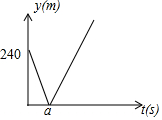 甲,乙两人沿同一条滨海大道同起点、同方向进行体育锻炼,已知甲匀速跑步,先出发60s,乙匀速骑车,速度是甲的两倍,在锻炼的过程中,设甲乙两人相距y(m),乙骑车的时间为t(s),y是t的函数,其图象的一部分如图所示.
甲,乙两人沿同一条滨海大道同起点、同方向进行体育锻炼,已知甲匀速跑步,先出发60s,乙匀速骑车,速度是甲的两倍,在锻炼的过程中,设甲乙两人相距y(m),乙骑车的时间为t(s),y是t的函数,其图象的一部分如图所示.
 如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-$\frac{1}{2}$x-6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-$\frac{1}{2}$x-6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.