题目内容
10. 如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-$\frac{1}{2}$x-6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-$\frac{1}{2}$x-6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求$\frac{1}{2}$AM+CM它的最小值.
分析 (1)利用待定系数法求出抛物线解析式;
(2)先利用待定系数法求出直线AB的解析式,进而利用平行四边形的对边相等建立方程求解即可;
(3)①先判断出要以点A,E,F,H为顶点的四边形是矩形,只有EF为对角线,利用中点坐标公式建立方程即可;
②先取EG的中点P进而判断出△PEM∽△MEA即可得出PM=$\frac{1}{2}$AM,连接CP交圆E于M,再求出点P的坐标即可得出结论.
解答 解:(1)∵点A(-4,-4),B(0,4)在抛物线y=-x2+bx+c上,
∴$\left\{\begin{array}{l}{-16-4b+c=-4}\\{c=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=-2}\\{c=4}\end{array}\right.$,
∴抛物线的解析式为y=-x2-2x+4;
(2)设直线AB的解析式为y=kx+n过点A,B,
∴$\left\{\begin{array}{l}{n=4}\\{-4k+n=-4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=2}\\{n=4}\end{array}\right.$,
∴直线AB的解析式为y=2x+4,
设E(m,2m+4),
∴G(m,-m2-2m+4),
∵四边形GEOB是平行四边形,
∴EG=OB=4,
∴-(-m2-2m+4-2m-4)=4,
∴m=-2
∴G(-2,4).
(3)①如图1,
由(2)知,直线AB的解析式为y=2x+4,
∴设E(a,2a+4),
∵直线AC:y=-$\frac{1}{2}$x-6,
∴F(a,-$\frac{1}{2}$a-6),
设H(0,p),
∵以点A,E,F,H为顶点的四边形是矩形,
∵直线AB的解析式为y=2x+4,直线AC:y=-$\frac{1}{2}$x-6,
∴AB⊥AC,
∴EF为对角线,
∴$\frac{1}{2}$(-4+0)=$\frac{1}{2}$(a+a),$\frac{1}{2}$(-4+p)=$\frac{1}{2}$(2a+4-$\frac{1}{2}$a-6),
∴a=-2,P=-1,
∴E(-2,0).H(0,-1);
②如图2,
由①知,E(-2,0),H(0,-1),A(-4,-4),
∴EH=$\sqrt{5}$,AE=2$\sqrt{5}$,
设AE交⊙E于G,取EG的中点P,
∴PE=$\frac{\sqrt{5}}{2}$,
连接PC交⊙E于M,连接EM,
∴EM=EH=$\sqrt{5}$,
∴$\frac{PE}{ME}=\frac{\frac{\sqrt{5}}{2}}{\sqrt{5}}$=$\frac{1}{2}$,
∵$\frac{ME}{AE}=\frac{\sqrt{5}}{2\sqrt{5}}$=$\frac{1}{2}$,
∴$\frac{PE}{ME}=\frac{ME}{AE}$=$\frac{1}{2}$,∵∠PEM=∠MEA,
∴△PEM∽△MEA,
∴$\frac{PM}{AM}=\frac{ME}{AE}=\frac{1}{2}$,
∴PM=$\frac{1}{2}$AM,
∴$\frac{1}{2}$AM+CM的最小值=PC,
设点P(p,2p+4),
∵E(-2,0),
∴PE2=(p+2)2+(2p+4)2=5(p+2)2,
∵PE=$\frac{\sqrt{5}}{2}$,
∴5(p+2)2=$\frac{5}{4}$,
∴p=-$\frac{5}{2}$或p=-$\frac{3}{2}$(由于E(-2,0),所以舍去),
∴P(-$\frac{5}{2}$,-1),
∵C(0,-6),
∴PC=$\sqrt{(-\frac{5}{2})^{2}+(-1+6)^{2}}$=$\frac{5\sqrt{5}}{2}$,
即:$\frac{1}{2}$AM+CM=$\frac{5\sqrt{5}}{2}$.
点评 此题是二次函数综合题,主要考查了待定系数法,平行四边形的性质,矩形的性质,相似三角形的判定和性质,中点坐标公式,极值的确定,解(1)的关键是掌握待定系数法,解(2)的关键是利用平行四边形的对边相等建立方程求解,解(3)①的关键是利用中点坐标公式建立方程求解,解(3)②的关键是构造相似三角形,是一道中等难度的题目.

 阅读快车系列答案
阅读快车系列答案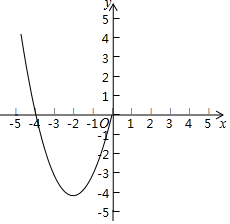 某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | -3 | -4 | -3 | 0 | -3 | … |
(2)根据表中数据,画出函数图象的另一部分;
(3)进一步探究函数图象,回答问题:
①观察图象可以得出,对应的方程x2-4|x|=0有3个实数根;
②关于x的方程x2-4|x|=a有2个实数根时,a的取值范围是a=-4或a>0;
③当x取何值时,y随x的增大而增大?
| A. | -2017 | B. | c | C. | 0 | D. | c-2017 |
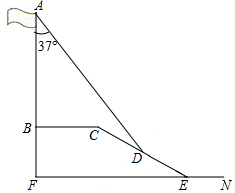 在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,$\sqrt{3}$≈1.73)
在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,$\sqrt{3}$≈1.73)| A. | 10.61 | B. | 10.52 | C. | 9.87 | D. | 9.37 |
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
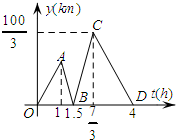 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图所示,已知乙比甲先出发1h.
 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为$\frac{4π}{3}$cm2.(结果保留π)
如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为$\frac{4π}{3}$cm2.(结果保留π)