题目内容
16. 如图,在平行四边形ABCD中,∠FCD=∠EAB,∠BCE=∠DAF,求证:四边形FAEC是平行四边形.
如图,在平行四边形ABCD中,∠FCD=∠EAB,∠BCE=∠DAF,求证:四边形FAEC是平行四边形.
分析 由四边形ABCD是平行四边形,可得AB∥CD,AD∥BC,∠BAD=∠BCD,即可得∠ADF=∠CBE,∠CDF=∠ABE,又由∠FCD=∠EAB,∠BCE=∠DAF,利用三角形的外角的性质以及角的和差,即可证得∠EAF=∠ECF,∠AFC=∠AEC,则可得四边形FAEC是平行四边形.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,∠BAD=∠BCD,
∴∠ADF=∠CBE,∠CDF=∠ABE,
∵∠FCD=∠EAB,∠BCE=∠DAF,
又∵∠EAF=∠BAD-∠DAF-∠EAB,∠ECF=∠BCD-∠FCD-∠BCE,
∴∠EAF=∠ECF,
∵∠AFC=∠AFE+∠EFC=(∠ADF+∠DAF)+(∠FCD+∠CDF),∠AEC=∠AEF+∠CEF=(∠EAB+∠ABE)+(∠CBE+∠BCE),
∴∠AFC=∠AEC,
∴四边形FAEC是平行四边形.
点评 此题考查了平行四边形的判定与性质.注意有两组对角分别相等的四边形是平行四边形.

练习册系列答案
相关题目
11.某社区计划购买甲乙两种树苗共600棵,甲,乙两种树苗单价及成活率见下表:
(1)购买树苗资金刚好44000元,可购买甲乙树苗多少棵?
(2)若这批树苗的成活率为90%,则应购买甲、乙两种树苗各多少棵?
| 种类 | 单价 | 成活率 |
| 甲 | 60 | 88% |
| 乙 | 80 | 96% |
(2)若这批树苗的成活率为90%,则应购买甲、乙两种树苗各多少棵?
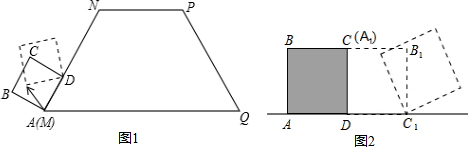
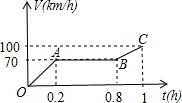 一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:
一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法: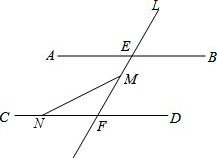 如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)
如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)