题目内容
19.计算:(1)(a-b)2-a(a-3b)
(2)($\frac{{x}^{2}-9}{{x}^{2}-6x+9}$+$\frac{1}{3-x}$)÷(-$\frac{5}{x-3}$-x-3)
分析 (1)根据完全平方公式和单项式乘多项式可以解答本题;
(2)根据分式的加法和减法、除法可以解答本题.
解答 解:(1)(a-b)2-a(a-3b)
=a2-2ab+b2-a2+3ab
=ab+b2;
(2)($\frac{{x}^{2}-9}{{x}^{2}-6x+9}$+$\frac{1}{3-x}$)÷(-$\frac{5}{x-3}$-x-3)
=[$\frac{(x+3)(x-3)}{(x-3)^{2}}+\frac{1}{3-x}$]÷[$\frac{-5-(x+3)(x-3)}{x-3}$]
=$\frac{x+3-1}{x-3}•\frac{x-3}{-(x+2)(x-2)}$
=$\frac{x-2}{-(x+2)(x-2)}$
=$-\frac{1}{x+2}$.
点评 本题考查分式的混合运算、完全平方公式、单项式乘多项式,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
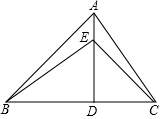 如图,锐角△ABC中,∠ABC=45°,AD是高,E为AD上一点,BE=AC.
如图,锐角△ABC中,∠ABC=45°,AD是高,E为AD上一点,BE=AC.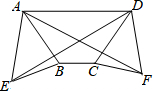 如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连AF,DE.求证:AF=DE.
如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连AF,DE.求证:AF=DE. 如图所示,在平面直角坐标系中,OA1=1,将OA1以O为旋转中心逆时针旋转90°到y轴OA2处,然后半径增加1个单位长度到A3,将OA3再以点O为旋转中心逆时针旋转90°到x轴OA4处,然后半径增加1个单位长度到A5,…,按图中规律进行下去,则点A2017的坐标为(1010,0).
如图所示,在平面直角坐标系中,OA1=1,将OA1以O为旋转中心逆时针旋转90°到y轴OA2处,然后半径增加1个单位长度到A3,将OA3再以点O为旋转中心逆时针旋转90°到x轴OA4处,然后半径增加1个单位长度到A5,…,按图中规律进行下去,则点A2017的坐标为(1010,0).