题目内容
14.如图1,已知抛物线y=-x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).(1)求抛物线的函数表达式;
(2)点P是抛物线上位于第一象限内的动点,是否存在点P,使△PBC得面积最大,若存在,请求出点P的坐标和△PBC面积的最大值;若不存在,请说明理由;
(3)如图2,直线l经过A、C两点,点Q时位于y轴左侧的抛物线上的一动点,经过点B和点Q的直线m,与y轴相交于点M,与直线l相交于点N,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
分析 (1)把B、C两点的坐标代入抛物线的解析式得到关于b、c的方程组,然后求得b、c的值即可;
(2)连结BC,过点P作y轴的平行线,交BC与点M,交x轴与点H,先求得BC的解析式为y=-x+3,设点P的坐标为(x,-x2+2x+3)则点M的坐标为(x,-x+3),然后由S△PBC=$\frac{1}{2}$PM•(OH+HB)列出△PBC的面积与x的函数关系式可求得当x=$\frac{3}{2}$时,三角形的面积有最大值,从而可得到点P的坐标;
(3)如图2所示:直线m1交y轴于点M1,交直线l于点N1,先证明△ACO≌△M1BO,从而得到OM1=OA=1,于是可得到点M1(0,1),然后求得直线BM1的解析式即可,直线m2交y轴与点M2,交直线l于点N2时,同理可求得点M2的坐标为(0,-1).,然后再求得直线BM2的解析式即可.
解答 解:(1)把B、C两点的坐标代入抛物线的解析式得:$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3.
(2)存在.
如图1所示:连结BC,过点P作y轴的平行线,交BC与点M,交x轴与点H.
设BC的解析式为y=kx+b,将B(3,0),C(0,3)代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,解得:k=-1,b=3,
∴直线BC的解析式为y=-x+3.
设点P的坐标为(x,-x2+2x+3)则点M的坐标为(x,-x+3).
∴PM=-x2+2x+3-(-x+3)=-x2+3x.
∴S△PBC=$\frac{1}{2}$PM•(OH+HB)=$\frac{1}{2}$PM•OB=-$\frac{3}{2}$x2+$\frac{9}{2}$x=-$\frac{3}{2}$(x-$\frac{3}{2}$)2+$\frac{27}{8}$.
∴点P的坐标为($\frac{3}{2}$,$\frac{15}{4}$).
(3)存在.
如图2所示: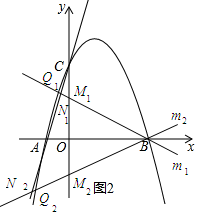
直线m1交y轴于点M1,交直线l于点N1.
当△AN1B和△M1N1C相似时,则∠AN1B=∠M1N1C.
∵∠AN1B+∠M1N1C=180°,
∴∠AN1B=∠M1N1C=90°.
∴∠ACO=∠M1BO.
在△AOC和△M1BO中,$\left\{\begin{array}{l}{∠AOC=∠{M}_{1}OB}\\{OC=OB}\\{∠ACO=∠{M}_{1}BO}\end{array}\right.$,
∴△ACO≌△M1BO.
∴OM1=OA.
∵A(-1,0),
∴OM1=OA=1.
∴点M1(0,1).
由M1(0,1),B(3,0),
∴直线m1的解析式为y=-$\frac{1}{3}$x+1.
直线m2交y轴与点M2,交直线l于点N2时.
∵△AN2B和△M2N2C相似时,必有∠AN2B=∠M2N2C.
同理:可得到△ACO≌△M2BO.
∴OM2=OA.
∴点M2的坐标为(0,-1).
∴直线BM2的解析式为y=$\frac{1}{3}$x-1.
综上所述,满足条件的直线m的解析式为y=-$\frac{1}{3}$x+1或y=$\frac{1}{3}$x-1.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、二次函数的性质、相似三角形的性质、全等三角形的性质,证得△ACO≌△M1BO、△ACO≌△M2BO是解题的关键.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案| 有人和你打招呼,你笔直向他走过去 | 两点之间线段最短 |
| 要用两个钉子把毛巾架安装在墙上 | 两点确定一条直线 |
| 桥建造的方向通常是垂直于河两岸 | 夹在两平行线间的线段中,垂线段最短 |
| 人去河边打水总是垂直于河边方向走 | 直线外一点和直线上各点的连线中,垂线段最短 |
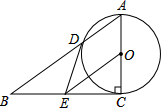 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E为BC的中点,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E为BC的中点,连接DE. 如图,已知在△ABC中,点D,E,F分别在BC,AB,AC边上.
如图,已知在△ABC中,点D,E,F分别在BC,AB,AC边上.