题目内容
11.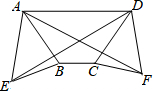 如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连AF,DE.求证:AF=DE.
如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连AF,DE.求证:AF=DE.
分析 先判断梯形ABCD为等腰梯形得到∠BAD=∠CDA,再根据等边三角形的性质得AE=AB,DF=CD,∠BAE=∠CDF=60°,从而得到AE=DF,∠DAE=∠ADF,然后利用“SAS”证明△DAE≌△ADF,从而得到AF=DE.
解答 证明:∵AD∥BC,AB=CD,
∴梯形ABCD为等腰梯形,
∴∠BAD=∠CDA,
又∵△ABE和△DCF是等边三角形,
∴AE=AB,DF=CD,∠BAE=∠CDF=60°,
∴AE=DF,∠DAE=∠ADF,
在△DAE和△ADF中
$\left\{\begin{array}{l}{AD=DA}\\{∠DAE=∠ADF}\\{AE=DF}\end{array}\right.$
∴△DAE≌△ADF,
∴AF=DE.
点评 本题考查了梯形:一组对边平行,另一组对边不平行的四边形叫做梯形.两腰相等的梯形叫做等腰梯形.也考查了全等三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.写出日常生活现象中的数学原理:
| 有人和你打招呼,你笔直向他走过去 | 两点之间线段最短 |
| 要用两个钉子把毛巾架安装在墙上 | 两点确定一条直线 |
| 桥建造的方向通常是垂直于河两岸 | 夹在两平行线间的线段中,垂线段最短 |
| 人去河边打水总是垂直于河边方向走 | 直线外一点和直线上各点的连线中,垂线段最短 |
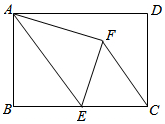 如图,在矩形ABCD中,AB=5,BC=8,点E为BC上一动点,把△ABE沿AE折叠;若点E是BC边的中点,点B落在点F处,连接CF.
如图,在矩形ABCD中,AB=5,BC=8,点E为BC上一动点,把△ABE沿AE折叠;若点E是BC边的中点,点B落在点F处,连接CF.