题目内容
13.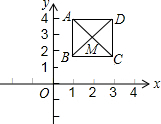 如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).
如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).
分析 首先由正方形ABCD,顶点A(1,4),B(1,2),C(3,2),然后根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标,即可得规律:第n次变换后的点M的对应点的坐标为:当n为奇数时为(2+n,-3),当n为偶数时为(2+n,3),继而求得把正方形ABCD连续经过2015次这样的变换得到正方形ABCD的对角线交点M的坐标.
解答 解:∵正方形ABCD,顶点A(1,4),B(1,2),C(3,2),
∴对角线交点M的坐标为(2,3),
根据题意得:第1次变换后的点M的对应点的坐标为(2+1,-3),即(3,-3),
第2次变换后的点M的对应点的坐标为:(2+2,3),即(4,3),
第3次变换后的点M的对应点的坐标为(2+3,-3),即(5,-3),
第n次变换后的点M的对应点的坐标为:当n为奇数时为(2+n,-3),当n为偶数时为(2+n,3),
∴连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为(2017,-3).
故答案为(2017,-3).
点评 此题考查了点的坐标变化,对称与平移的性质.得到规律:第n次变换后的对角线交点M的对应点的坐标为:当n为奇数时为(2+n,-3),当n为偶数时为(2+n,3)是解此题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
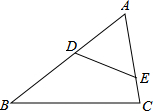 △ABC中,点D,E分别在AB,AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为5,求边AB的长.
△ABC中,点D,E分别在AB,AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为5,求边AB的长.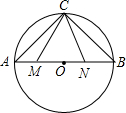 如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
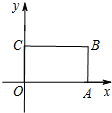
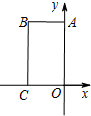
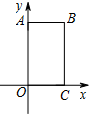
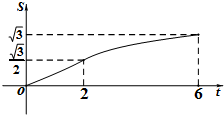 在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )
在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )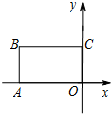
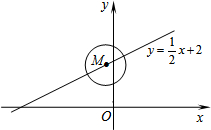 ⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).
⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).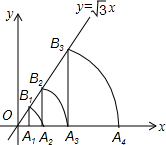 如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).
如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).