题目内容
1.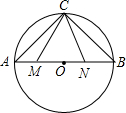 如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
分析 作DA⊥AB,使DA=BN,连接DC,DM,根据旋转的性质求得∠ACD=∠BCN,DC=NC,然后证得△DMC≌△NMC,求得DM=MN=6,设AM=x;则AD=BN=AB-AM-MN=7-x,根据勾股定理得出x2+(7-x)2=36,进而就可求得线段AM的长度.
解答 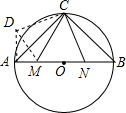 解:作DA⊥AB,使DA=BN,连接DC,DM,
解:作DA⊥AB,使DA=BN,连接DC,DM,
∵线段AB是⊙O的直径,点C是弧AB的中点,
∴$\widehat{AC}$=$\widehat{BC}$,∠ACB=90°,
∴AC=BC,
∴∠CAB=∠CBA=45°,
∴∠DAC=∠NBC=45°,
在△ADC和△NCB中,
$\left\{\begin{array}{l}{AD=NB}\\{∠DAC=∠NBC}\\{AC=BC}\end{array}\right.$
∴△ADC≌△NCB(SAS),
∴∠ACD=∠BCN,DC=NC,
∵∠MCN=45°
∴∠ACM+∠BCN=45°
∴∠ACM+∠ACD=45°
即∠MCD=45°=∠MCN,
在△DMC和△NMC中,
$\left\{\begin{array}{l}{DC=CN}\\{∠MCD=∠MCN}\\{CM=CM}\end{array}\right.$
∴△DMC≌△NMC(SAS),
∴DM=MN=6,
设AM=x;则AD=BN=AB-AM-MN=7-x
根据勾股定理
AM2+AD2=DM2
x2+(7-x)2=36
2x2-14x+13=0,解得x=$\frac{7±\sqrt{23}}{2}$,
∴AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
故答案为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
点评 本题考查了旋转的性质,三角形全等的判定和性质,等腰直角三角形的性质,勾股定理的应用等,作出辅助线构建全等三角形是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | x3•x2=x5 | B. | (x3)2=x5 | C. | (x+1)2=x2+1 | D. | (2x)2=2x2 |
| A. | ($\sqrt{3}$,-1) | B. | (-1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (1,-$\sqrt{3}$) |

| A. | 2 | B. | $\frac{π}{2}$ | C. | $\frac{π}{2}$+1 | D. | $\frac{π}{2}$+3 |
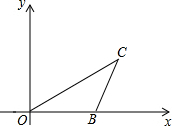 已知B(4,0),C(5,2),把△OBC绕O点逆时针旋转90°,得到△OB′C′,
已知B(4,0),C(5,2),把△OBC绕O点逆时针旋转90°,得到△OB′C′,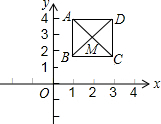 如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).
如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).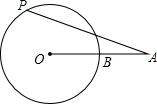 如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是30°.
如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是30°.