题目内容
4.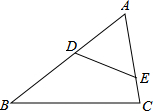 △ABC中,点D,E分别在AB,AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为5,求边AB的长.
△ABC中,点D,E分别在AB,AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为5,求边AB的长.
分析 由∠AED=∠B,∠A是公共角,根据有两角对应相等的三角形相似,即可证得△ADE∽△ACB,又由相似三角形面积的比等于相似比的平方,即可得$\frac{{S}_{△ADE}}{{S}_{△ABC}}=(\frac{AE}{AB})^{2}$,然后由AE=2,△ADE的面积为4,四边形BCDE的面积为5,即可求得AB的长.
解答 解:∵∠AED=∠B,∠A是公共角,
∴△ADE∽△ACB,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=(\frac{AE}{AB})^{2}$,
∵△ADE的面积为4,四边形BCED的面积为5,
∴△ABC的面积为9,
∵AE=2,
∴$\frac{4}{9}=(\frac{2}{AB})^{2}$,
解得:AB=3.
点评 此题考查了相似三角形的判定与性质.此题比较简单,注意掌握有两角对应相等的三角形相似与相似三角形面积的比等于相似比的平方定理的应用.

练习册系列答案
相关题目
4.-2-1的结果是( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
1.下列运算正确的是( )
| A. | x3•x2=x5 | B. | (x3)2=x5 | C. | (x+1)2=x2+1 | D. | (2x)2=2x2 |
16.在平面直角坐标系中,点($\sqrt{3}$,1)绕原点顺时针旋转60°后得到点( )
| A. | ($\sqrt{3}$,-1) | B. | (-1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (1,-$\sqrt{3}$) |
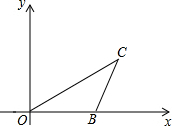 已知B(4,0),C(5,2),把△OBC绕O点逆时针旋转90°,得到△OB′C′,
已知B(4,0),C(5,2),把△OBC绕O点逆时针旋转90°,得到△OB′C′,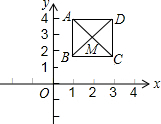 如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).
如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3). 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.