题目内容
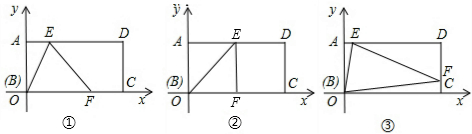
18.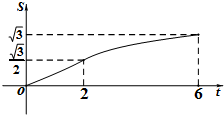 在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )
在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )| A. |  | B. |  | C. | 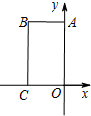 | D. | 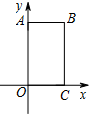 |
分析 根据图象计算0秒、2秒、6秒的时候,矩形在第二象限内的面积为S,即可分析出矩形OABC的初始位置.
解答 解:由图象可以看出在0秒时,S=0,在2秒时,S=$\frac{\sqrt{3}}{2}$,在6秒时,S=$\sqrt{3}$;由题意知,矩形OABC绕原点0以每秒15°的速度逆时针旋转,6秒逆时针旋转90°,S=$\sqrt{3}$,不难发现B和D都符合,但在2秒时,S=$\frac{\sqrt{3}}{2}$,即矩形OABC绕原点0逆时针旋转30°时,S=$\frac{\sqrt{3}}{2}$,则只有D符合条件.
故选:D.
点评 本题主要考查了函数的图象以及旋转问题,正确分析0秒、2秒、6秒时图形的位置和图形在第二象限的面积是解决问题的关键.

练习册系列答案
相关题目
6.如图,A,B,C,D为圆O的四等分点,动点P从圆心O出发,沿O-C-D-O-C-D-O路线作匀速运动,设运动时间为x(秒),∠APB的度数为y(度),右图函数图象表示y与x之间函数关系,则点M的横坐标应为( )


| A. | 2 | B. | $\frac{π}{2}$ | C. | $\frac{π}{2}$+1 | D. | $\frac{π}{2}$+3 |
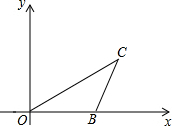 已知B(4,0),C(5,2),把△OBC绕O点逆时针旋转90°,得到△OB′C′,
已知B(4,0),C(5,2),把△OBC绕O点逆时针旋转90°,得到△OB′C′,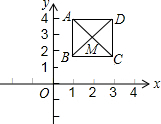 如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).
如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).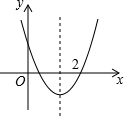 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列有4个结论:①b2-4ac>0;②abc<0;③b<a+c;④4a+b=1.请你将正确结论的番号都写出来①②③.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列有4个结论:①b2-4ac>0;②abc<0;③b<a+c;④4a+b=1.请你将正确结论的番号都写出来①②③.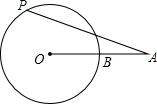 如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是30°.
如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是30°.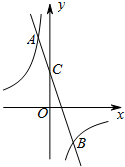 如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=-$\frac{6}{x}$的图象交于A(-1,m),B(n,-3)两点,一次函数y=kx+b的图象与y轴交于点C.
如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=-$\frac{6}{x}$的图象交于A(-1,m),B(n,-3)两点,一次函数y=kx+b的图象与y轴交于点C.