题目内容
5.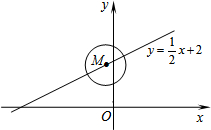 ⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).
⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).
分析 设当⊙M与y轴相切时圆心M的坐标为(x,$\frac{1}{2}$x+2),再根据⊙M的半径为1即可得出y的值.
解答 解:∵⊙M的圆心在一次函数y=$\frac{1}{2}$x+2的图象上运动,
∴设当⊙M与y轴相切时圆心M的坐标为(x,$\frac{1}{2}$x+2),
∵⊙M的半径为1,
∴x=1或x=-1,
当x=1时,y=$\frac{5}{2}$,
当x=-1时,y=$\frac{3}{2}$.
∴P点坐标为:(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).
故答案为:(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).
点评 本题考查的是一次函数综合题,熟知直线与圆相切的性质是解答此题的关键.

练习册系列答案
相关题目
4.-2-1的结果是( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
16.在平面直角坐标系中,点($\sqrt{3}$,1)绕原点顺时针旋转60°后得到点( )
| A. | ($\sqrt{3}$,-1) | B. | (-1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (1,-$\sqrt{3}$) |
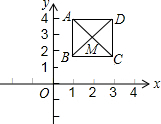 如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).
如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).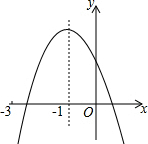 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )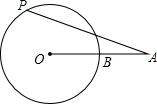 如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是30°.
如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是30°.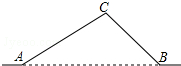 如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.
如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路. 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F. 如图是由6个相同的小正方体组成的几何体,那么这个几何体的俯视图是( )
如图是由6个相同的小正方体组成的几何体,那么这个几何体的俯视图是( )


