题目内容
2．解不等式组$\left\{\begin{array}{l}{2（x+2）＞3x}\\{\frac{3x-1}{2}≥-2}\end{array}\right.$并将它的解集在数轴上表示出来．分析 分别求出每个不等式的解集，在根据“大小小大中间找”即可得答案．
解答 解：解不等式2（x+2）＞3x，得：x＜4，
解不等式$\frac{3x-1}{2}$≥-2，得：x≥-1，
∴不等式组的解集为-1≤x＜4，
将解集表示在数轴上如下：
点评 本题主要考查解一元一次不等式组的能力，熟练掌握解一元一次不等式组的基本步骤是解题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
13．
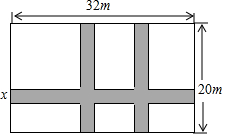如图，在长为32m，宽为20m的矩形空地内，修三条同样宽的道路（阴影部分的矩形为空地内的道路），所修的道路将这块空地分成六块，如果在空地上道路以外的部分种上花草，并且保证种花草的面积是570m2，问道路应多宽？设道路的宽为xm，则下面所列方程正确的是（ ）
如图，在长为32m，宽为20m的矩形空地内，修三条同样宽的道路（阴影部分的矩形为空地内的道路），所修的道路将这块空地分成六块，如果在空地上道路以外的部分种上花草，并且保证种花草的面积是570m2，问道路应多宽？设道路的宽为xm，则下面所列方程正确的是（ ）| A． | （32-x）（20-x）=32×20-570 | B． | 32x+2×20x=32×20-570 | ||
| C． | （32-2x）（20-x）=570 | D． | 32x+2×20x-2x2=570 |
10．在-1，0，1，2，3这五个数中任取两数m，n，则二次函数y=-（x+m）2-n的顶点在x轴上的概率为（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{1}{4}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{2}$ |
11．小明想用最大刻度为100℃的温度计测量食用油的沸点温度（远高于100℃），显然不能直接测量，于是他想到了另一种方法．把常温10℃的食用油放在锅内用煤气灶均匀地加热，开始加热后，每隔10s测量一次油温，共测量了4次，测得的数据如下：
他测量出把油烧到沸腾所需要的时间是160s，这样就可以确定该食用油的温度．
（1）写出w与r的函数解析式．
（2）求这种食用油沸点的温度．
| 时间t/s | 0 | 10 | 20 | 30 |
| 油温w/℃ | 10 | 25 | 40 | 55 |
（1）写出w与r的函数解析式．
（2）求这种食用油沸点的温度．