题目内容
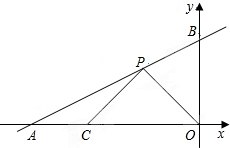 如图,直线AB与x轴、y轴分别交于点A(-6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(-4,0).
如图,直线AB与x轴、y轴分别交于点A(-6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(-4,0).(1)求直线AB所对应的函数关系式;
(2)设动点P的坐标为(m,n),△PAC的面积为S.
①当PC=PO时,求点P的坐标;
②写出S与m的函数关系式及自变量m的取值范围;并求出使S△PAC=S△PBO时,点P的坐标.
考点:一次函数综合题
专题:
分析:(1)利用待定系数法求出函数解析式即可;
(2)①根据PC=PO,利用点P在CO的垂直平分线上,求出P点坐标;
②将点P(m,n)代入y=
x+3得,n=
m+3,根据S△PAC=S△PBO,得到关于m的解析式,求出P点坐标.
(2)①根据PC=PO,利用点P在CO的垂直平分线上,求出P点坐标;
②将点P(m,n)代入y=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)设直线AB所对应函数关系式为y=kx+b,
把A(-6,0)、B(0,3)代入解析式得,
,解得
;
直线AB所对应的函数关系式为y=
x+3.
(2)①∵PC=PO,
∴点P在CO的垂直平分线上,
∵点C的坐标为(-4,0),
∴点P的横坐标为-2,
∴n=
×(-2)+3=2,
∴点P的横坐标为(-2,2).
②将点P(m,n)代入y=
x+3得,n=
m+3,
∴S=
AC•n=
×2n=n=
m+3,(-6<m<0).
∵S△PAC=S△PBO,
∴
m+3=
×3×|m|,
即
m+3=-
×3×m,
解得m=-
,
∴P(-
,
).
把A(-6,0)、B(0,3)代入解析式得,
|
|
直线AB所对应的函数关系式为y=
| 1 |
| 2 |
(2)①∵PC=PO,
∴点P在CO的垂直平分线上,
∵点C的坐标为(-4,0),
∴点P的横坐标为-2,
∴n=
| 1 |
| 2 |
∴点P的横坐标为(-2,2).
②将点P(m,n)代入y=
| 1 |
| 2 |
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△PAC=S△PBO,
∴
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得m=-
| 3 |
| 2 |
∴P(-
| 3 |
| 2 |
| 9 |
| 4 |
点评:本题考查了一次函数综合题,熟悉待定系数法、垂直平分线的性质、三角形的面积公式是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
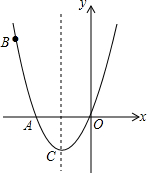 如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.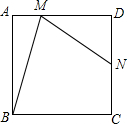 如图,在正方形ABCD中,N是DC的中点,M是AD上异于D点的任一点,且∠NMB=∠MBC.
如图,在正方形ABCD中,N是DC的中点,M是AD上异于D点的任一点,且∠NMB=∠MBC. 如图,过圆周上一点P作直径AB的垂线PM,M为垂足,过P及A作圆的切线交于Q,BQ交PM于N,求证:PN=MN.
如图,过圆周上一点P作直径AB的垂线PM,M为垂足,过P及A作圆的切线交于Q,BQ交PM于N,求证:PN=MN. 如图,已知直线AB、CD相交于点O,OB平分∠DOE,∠DOE=80°,则∠AOC=
如图,已知直线AB、CD相交于点O,OB平分∠DOE,∠DOE=80°,则∠AOC=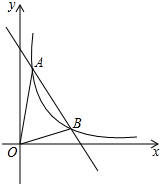 如图,一次函数y=-2x+8与反比例函数y=
如图,一次函数y=-2x+8与反比例函数y=