题目内容
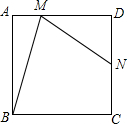 如图,在正方形ABCD中,N是DC的中点,M是AD上异于D点的任一点,且∠NMB=∠MBC.
如图,在正方形ABCD中,N是DC的中点,M是AD上异于D点的任一点,且∠NMB=∠MBC.若DN=1,则BM的长为
考点:正方形的性质,勾股定理
专题:
分析:延长MN于K,根据正方形的性质结合N是DC的中点,得出AD=2,MD=CK,MN=NK,根据∠NMB=∠MBC.得出MK=BK=BC+CK,设CK=MD=x,则MK=2+x,MN=1+
x,在RT△MND中,根据勾股定理求得x的值,进而求得AM的值,在RT△MAB中根据勾股定理即可求得BM的值.
| 1 |
| 2 |
解答: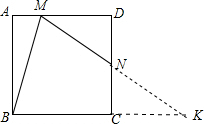 解:延长MN交BC的延长线于K,
解:延长MN交BC的延长线于K,
∵在正方形ABCD中,N是DC的中点,
∴AD=DC=DN+NC=2DN=2,AD∥BC,
在△MND与△KNC中,
,
∴△MND≌△KNC(AAS),
∴MD=CK,MN=NK,
∵∠NMB=∠MBC.
∴MK=BK=BC+CK,
设CK=MD=x,
∴MK=2+x,MN=1+
x,
在RT△MND中,x2+12=(1+
x)2,
解得x=
,x=0(舍去),
∴AM=2-
=
,
在RT△MAB中,BM2=AB2+AM2=4+
=
,
∴BM=
.
故答案为
.
 解:延长MN交BC的延长线于K,
解:延长MN交BC的延长线于K,∵在正方形ABCD中,N是DC的中点,
∴AD=DC=DN+NC=2DN=2,AD∥BC,
在△MND与△KNC中,
|
∴△MND≌△KNC(AAS),
∴MD=CK,MN=NK,
∵∠NMB=∠MBC.
∴MK=BK=BC+CK,
设CK=MD=x,
∴MK=2+x,MN=1+
| 1 |
| 2 |
在RT△MND中,x2+12=(1+
| 1 |
| 2 |
解得x=
| 4 |
| 3 |
∴AM=2-
| 4 |
| 3 |
| 2 |
| 3 |
在RT△MAB中,BM2=AB2+AM2=4+
| 4 |
| 9 |
| 40 |
| 9 |
∴BM=
| 2 |
| 3 |
| 10 |
故答案为
| 2 |
| 3 |
| 10 |
点评:本题考查了正方形的性质,勾股定理的应用,作出辅助线构建等腰三角形是本题的关键.

练习册系列答案
相关题目
?ABCD的对角线AC、BD相交于O,AC=4,BD=5,BC=3,则△BOC的周长为( )
| A、7.5 | B、12 |
| C、6 | D、无法确定 |
在下列各数中是无理数的有( )
-0.333…,
,
,3π,3.141 5,2.010 101…(相邻两个1之间有1个0).
-0.333…,
| 4 |
| 5 |
| A、2个 | B、3个 | C、4个 | D、5个 |
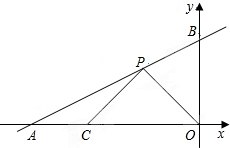 如图,直线AB与x轴、y轴分别交于点A(-6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(-4,0).
如图,直线AB与x轴、y轴分别交于点A(-6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(-4,0).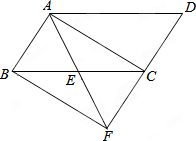 如图,在?ABCD中,E是BC的中点,连结AE并延长,交DC的延长线于点F.
如图,在?ABCD中,E是BC的中点,连结AE并延长,交DC的延长线于点F.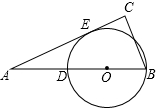 如图,在Rt△ABC中,∠C=90°,D是AB上的一点,以BD为直径的⊙O切AC于点E,AE=4,AD=2,求⊙O半径.
如图,在Rt△ABC中,∠C=90°,D是AB上的一点,以BD为直径的⊙O切AC于点E,AE=4,AD=2,求⊙O半径.