题目内容
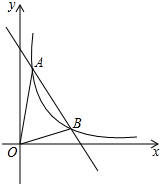 如图,一次函数y=-2x+8与反比例函数y=
如图,一次函数y=-2x+8与反比例函数y=| 6 |
| x |
(1)求△AOB的面积;
(2)直线y=-2x+8上有一点P,使得S△POA=3S△AOB,求P的坐标;
(3)直接写出反比例函数值大于一次函数值的自变量x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据解方程组,可得交点坐标,根据三角形的面积公式,可得答案;
(2)根据等底三角形的面积的关系,可得两三角形高的关系,根据解方程组,可得答案;
(3)根据反比例函数图象在一次函数图象上方的部分,是反比例函数值大于一次函数值,可得答案.
(2)根据等底三角形的面积的关系,可得两三角形高的关系,根据解方程组,可得答案;
(3)根据反比例函数图象在一次函数图象上方的部分,是反比例函数值大于一次函数值,可得答案.
解答:解:(1)一次函数y=-2x+8与反比例函数y=
(x>0)图象交于A、B两点,得
解得
,
,
A(1,6),B(3,2)
OA=
,B到直线OA:y=6x的距离是
,
△AOB的面积=
×
×
=2;
(2)直线y=-2x+8上有一点P,使得S△POA=3S△AOB,得
,
解得
或
.
∴P(5,-2)或p(-1,10),
(3)由图象得:当0<x<1或x>3时,反比例函数值大于一次函数值.
| 6 |
| x |
|
|
|
A(1,6),B(3,2)
OA=
| 37 |
4
| ||
| 37 |
△AOB的面积=
| 1 |
| 2 |
| 37 |
4
| ||
| 37 |
(2)直线y=-2x+8上有一点P,使得S△POA=3S△AOB,得
|
解得
|
|
∴P(5,-2)或p(-1,10),
(3)由图象得:当0<x<1或x>3时,反比例函数值大于一次函数值.
点评:本题考查了反比例函数与一次函数交点问题,利用了解方程组得出函数的交点,函数与不等式的关系.

练习册系列答案
相关题目
矩形周长为40,一边长为a,则表示矩形面积的代数式是( )
| A、a(20-a) |
| B、a(20+a) |
| C、a(40-a) |
| D、a(40-2a) |
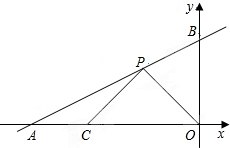 如图,直线AB与x轴、y轴分别交于点A(-6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(-4,0).
如图,直线AB与x轴、y轴分别交于点A(-6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(-4,0). 用尺规作图方法使下面的“破镜重圆”
用尺规作图方法使下面的“破镜重圆”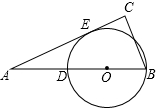 如图,在Rt△ABC中,∠C=90°,D是AB上的一点,以BD为直径的⊙O切AC于点E,AE=4,AD=2,求⊙O半径.
如图,在Rt△ABC中,∠C=90°,D是AB上的一点,以BD为直径的⊙O切AC于点E,AE=4,AD=2,求⊙O半径. 已知⊙O的内接正六边形的边长是2,则这个圆的半径是
已知⊙O的内接正六边形的边长是2,则这个圆的半径是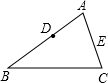 如图,在△ABC中,AB=12,AC=10,点D在AB上,且AD=4,在AC上取一点E,连结DE,使△ADE与原三角形相似.求AE的长.
如图,在△ABC中,AB=12,AC=10,点D在AB上,且AD=4,在AC上取一点E,连结DE,使△ADE与原三角形相似.求AE的长.