题目内容
已知a、b、c、为△ABC的三边长，且a2+b2=8a+12b-52，其中c是△ABC中最短的边长，且c为整数，求c的值．
考点：因式分解的应用,三角形三边关系
专题：
分析：由a2+b2=8a+12b-52，得a，b的值．进一步根据三角形一边边长大于另两边之差，小于它们之和，则b-a＜c＜a+b，即可得到答案．
解答：解：∵a2+b2=8a+12b-52
∴a2-8a+16+b2-12b+36=0
∴（a-4）2+（b-6）2=0
∴a=4，b=6
∴6-4＜c＜6+4
即 2＜c＜10．
∴整数c可取 3，4．
∴a2-8a+16+b2-12b+36=0
∴（a-4）2+（b-6）2=0
∴a=4，b=6
∴6-4＜c＜6+4
即 2＜c＜10．
∴整数c可取 3，4．
点评：此题考查了因式分解，以及三角形的三边关系，是一道综合性的题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
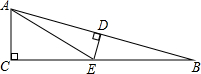如图，在△ABC中，∠C=90°，∠B=15°，D是AB的中点，DE⊥AB于D，交BC于E，则∠CAE的度数是（ ）| A、15° | B、30° |
| C、60° | D、75° |
如图，平面直角坐标系中，点A的坐标（6，0），点P在直线y=-2x+m上，且AP=OP=5，求m的值．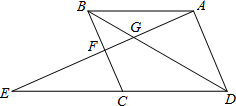
如图，点E为平行四边形ABCD中DC延长线上的一点，且CE=DC．连结AE，分别交BC、BD于点F、G．若BD=6，求DG的长．