题目内容
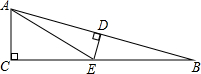如图，在△ABC中，∠C=90°，∠B=15°，D是AB的中点，DE⊥AB于D，交BC于E，则∠CAE的度数是（ ）| A、15° | B、30° |
| C、60° | D、75° |
考点：线段垂直平分线的性质
专题：
分析：先根据直角三角形的性质求出∠BAC的度数，再根据线段垂直平分线的性质求出∠EAB的度数，进而可得出结论．
解答：解：∵△ABC中，∠C=90°，∠B=15°，
∴∠BAC=90°-∠B=90°-15°=75°．
∵D是AB的中点，DE⊥AB于D，
∴AE=BE，
∴∠B=∠BAE=15°，
∴∠CAE=∠BAC-∠BAE=75°-15°=60°．
故选C．
∴∠BAC=90°-∠B=90°-15°=75°．
∵D是AB的中点，DE⊥AB于D，
∴AE=BE，
∴∠B=∠BAE=15°，
∴∠CAE=∠BAC-∠BAE=75°-15°=60°．
故选C．
点评：本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在△ABC中，D、E分别为AB、AC上两点，且BD=DE=EC，则图中面积相等的三角形有（ ）| A、4对 | B、5对 | C、6对 | D、7对 |
如图，已知线段AB=4，延长线段AB至C，使BC=2AB，点D是AC的中点，则DC=（ ）| A、5 | B、6 | C、7 | D、8 |
已知关于x，y的方程组
的解满足x+y=3，则k的值为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
下列从左到右的变形：
①5x2y=5yx2；②（a+b）（a-b）=a2-b2；③a2-2a+1=（a-1）2；④x2+3x=x（x+3），
其中是因式分解的个数是（ ）
①5x2y=5yx2；②（a+b）（a-b）=a2-b2；③a2-2a+1=（a-1）2；④x2+3x=x（x+3），
其中是因式分解的个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
不等式组
的所有整数解的和是（ ）
|
| A、-3 | B、-2 | C、0 | D、-5 |
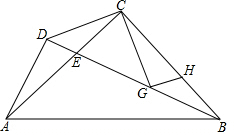如图△ABC中，CA=CB，∠ABC=90°，D为△ABC外一点，且AD⊥BD，BD交AC于E，G为BC上一点，且∠BCG=∠DCA，过G点作GH⊥CG交CB于H．