题目内容
16.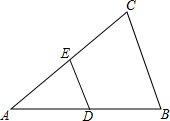 如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=$\frac{1}{2}$BC
如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=$\frac{1}{2}$BC求证:D、E分别是AB、AC的中点.
分析 如图,作BF∥AC交ED的延长线于点F,构建平行四边形BCEF,利用平行四边形的性质和全等三角形的判定定理AAS得到△ADE≌△BDF,则该全等三角形的 对应边相等:AD=BD,AE=BF=EC,即证得结论.
解答 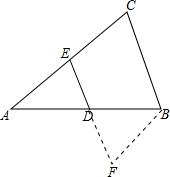 证明:作BF∥AC交ED的延长线于点F,
证明:作BF∥AC交ED的延长线于点F,
∵DE∥BC,
∴四边形BCEF是平行四边形,
∴BC=EF=2ED,AC∥BF,EC=BF,
∴ED=DF,∠A=∠DBF,
∴在△ADE与△BDF中,$\left\{\begin{array}{l}{∠A=∠DBF}\\{∠ADE=∠BDF}\\{DE=DF}\end{array}\right.$,
∴△ADE≌△BDF(AAS)
∴AD=BD,AE=BF=EC,即D、E分别是AB、AC的中点.
点评 本题考查了三角形中位线定理和全等三角形的判定与性质.注意:本题中辅助线的作法,通过作辅助线构建全等三角形是解题的难点.

练习册系列答案
相关题目
11.已知式子$\frac{{x}^{2}-4}{2x-4}$的值为零,则x的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
1.顺次连结对角线互相垂直的四边形各边中点所构成的四边形一定是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 不确定 |
8.直角三角形的两条直角边的长分别为5,12,则斜边上的高线的长为( )
| A. | $\frac{80}{13}$cm | B. | 13cm | C. | $\frac{13}{2}$cm | D. | $\frac{60}{13}$cm |
 如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD
如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD  已知:如图,?ABCD中,E、F分别是AD,BC的中点.求证:
已知:如图,?ABCD中,E、F分别是AD,BC的中点.求证: 如图,点E是矩形ABCD的边AD上一点,且BE=AD,如果AB=6,BC=10,求cos∠EBC的值.
如图,点E是矩形ABCD的边AD上一点,且BE=AD,如果AB=6,BC=10,求cos∠EBC的值.