题目内容
7. 如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD
如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD 求证:(1)△ABC≌△ABD;
(2)∠CEA=∠DEA.
分析 (1)首先利用“HL”证明Rt△ABC≌Rt△ABD,
(2)根据Rt△ABC≌Rt△ABD,得出∠CAB=∠DAB,进一步利用“SAS”证得△ACE≌△ADE,证得∠CEA=∠DEA.
解答 证明:(1)∵AC⊥BC,AD⊥BD,
∴∠ACB=∠ADB=90°,
在Rt△ABC和Rt△ABD中,
$\left\{\begin{array}{l}{AC=AD}\\{AB=AB}\end{array}\right.$,
∴Rt△ABC≌Rt△ABD(HL),
(2)∵Rt△ABC≌Rt△ABD,
∴∠CAB=∠DAB,
在△ACE和△ADE中,
$\left\{\begin{array}{l}{AC=AD}\\{∠CAE=∠DAE}\\{AE=AE}\end{array}\right.$,
∴△ACE≌△ADE,
∴∠CEA=∠DEA.
点评 本题考查三角形全等的判定与性质,结合图形,掌握基本的判定方法是解决问题的关键.

练习册系列答案
相关题目
12.根据下列条件,能判定平行四边形ABCD是矩形的是( )
| A. | AB=CD,AD=BC | B. | AB=BC | C. | AC=BD | D. | AB∥CD,AD∥BC |
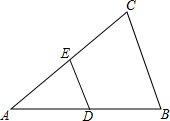 如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=$\frac{1}{2}$BC
如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=$\frac{1}{2}$BC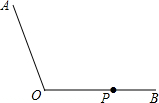 如图,已知点P为∠AOB一边OB上的一点.
如图,已知点P为∠AOB一边OB上的一点.