题目内容
8.直角三角形的两条直角边的长分别为5,12,则斜边上的高线的长为( )| A. | $\frac{80}{13}$cm | B. | 13cm | C. | $\frac{13}{2}$cm | D. | $\frac{60}{13}$cm |
分析 先利用勾股定理求出斜边长,再利用面积法求出斜边上的高即可.
解答 解:∵直角三角形的两条直角边的长分别为5,12,
∴斜边为$\sqrt{{5}^{2}+1{2}^{2}}$=13.
设h为斜边上的高.
∵S△ABC=$\frac{1}{2}$×5×12=$\frac{1}{2}$×13h,
∴h=$\frac{60}{13}$.
故选D.
点评 此题考查了勾股定理,以及三角形面积公式,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
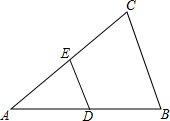 如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=$\frac{1}{2}$BC
如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=$\frac{1}{2}$BC 如图,已知点P为∠AOB一边OB上的一点.
如图,已知点P为∠AOB一边OB上的一点. 如图所示:∠1=30°,直线AB与CD相交于点O,已知,OE是∠BOC的平分线,则∠2=30°,∠3=75°.
如图所示:∠1=30°,直线AB与CD相交于点O,已知,OE是∠BOC的平分线,则∠2=30°,∠3=75°.