题目内容
1.顺次连结对角线互相垂直的四边形各边中点所构成的四边形一定是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 不确定 |
分析 根据四边形对角线互相垂直,运用三角形中位线平行于第三边证明四个角都是直角,进行判断即可.
解答  解:如图:∵E、F、G、H分别为各边中点
解:如图:∵E、F、G、H分别为各边中点
∴EF∥GH∥DB,EF=GH=$\frac{1}{2}$DB
EH=FG=$\frac{1}{2}$AC,EH∥FG∥AC
∵DB⊥AC
∴EF⊥EH
∴四边形EFGH是矩形.
故选:A.
点评 本题考查的是三角形中位线定理的应用,掌握三角形的中位线平行于第三边并且等于第三边的一半是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.根据下列条件,能判定平行四边形ABCD是矩形的是( )
| A. | AB=CD,AD=BC | B. | AB=BC | C. | AC=BD | D. | AB∥CD,AD∥BC |
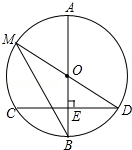 如图,已知AB是⊙O的直径,弦CD⊥AB于E,CD=16cm,BE=4cm,求:
如图,已知AB是⊙O的直径,弦CD⊥AB于E,CD=16cm,BE=4cm,求: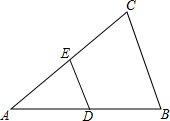 如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=$\frac{1}{2}$BC
如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=$\frac{1}{2}$BC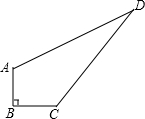 老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.
老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积. 如图,在Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=32°,则∠A的度数为58°.
如图,在Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=32°,则∠A的度数为58°. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为4和10,则b的面积为14.
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为4和10,则b的面积为14.