题目内容
6. 如图,点E是矩形ABCD的边AD上一点,且BE=AD,如果AB=6,BC=10,求cos∠EBC的值.
如图,点E是矩形ABCD的边AD上一点,且BE=AD,如果AB=6,BC=10,求cos∠EBC的值.
分析 由矩形的性质得出AD=BC,AD∥BC,∠A=90°,由勾股定理得出AE,由平行线的性质得出∠AEB=∠EBC,再由三角函数的定义即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠A=90°,
又∵BE=AD,BC=10,
∴BE=10,
∵∠A=90°
∴AB2+AE2=BE2,
∴AE=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵AD∥BC,
∴∠AEB=∠EBC,
∴cos∠EBC=cos∠AEB=$\frac{AE}{BE}$=$\frac{4}{5}$.
点评 本题考查了矩形的性质、勾股定理、平行线的性质、三角函数;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
14.二元一次方程4x+3y=25的自然数解有( )
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |
15.等腰三角形的两边长分别是4和5,则这个等腰三角形的周长是( )
| A. | 13或14 | B. | 13 | C. | 14 | D. | 无法确定 |
16.一箱啤酒(每箱24瓶)中有4瓶的盖内印有“奖”字,小明的爸爸买了一箱这种品牌的啤酒,但连续打开4瓶均未中奖,此时小明在剩下的啤酒中任意拿一瓶,那么他拿出的这瓶啤酒中奖的机会是( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
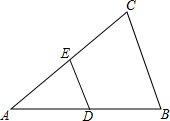 如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=$\frac{1}{2}$BC
如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=$\frac{1}{2}$BC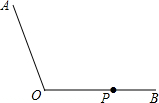 如图,已知点P为∠AOB一边OB上的一点.
如图,已知点P为∠AOB一边OB上的一点. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为4和10,则b的面积为14.
如图,直线l上有三个正方形a,b,c,若a,c的面积分别为4和10,则b的面积为14. 如图所示:∠1=30°,直线AB与CD相交于点O,已知,OE是∠BOC的平分线,则∠2=30°,∠3=75°.
如图所示:∠1=30°,直线AB与CD相交于点O,已知,OE是∠BOC的平分线,则∠2=30°,∠3=75°.