题目内容
11.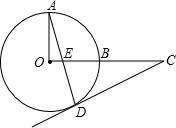 如图,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD交OC于点E.求证:CD=CE.
如图,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD交OC于点E.求证:CD=CE.
分析 连接OD,根据切线性质求出∠ODC=90°,求出∠A+∠AEO=∠ODA+∠EDC=90°,求出∠CED=∠EDC,根据等腰三角形的判定推出即可.
解答  证明:连接OD,
证明:连接OD,
∵OA⊥OB,CD切⊙O于D,
∴∠AOE=∠ODC=90°,
∴∠A+∠AEO=90°,∠ODA+∠CDE=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠AEO=∠EDC,
∵∠AEO=∠CED,
∴∠CED=∠EDC,
∴CD=CE.
点评 本题考查了切线的性质,等腰三角形的判定和性质,三角形内角和定理的应用,解此题的关键是能正确作出辅助线,并推出∠EDC=∠CED,题目比较好,难度适中.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
1. 如图,BD=CD,AE:DE=1:2,延长BE交AC于F,且AF=4cm,则AC的长为( )
如图,BD=CD,AE:DE=1:2,延长BE交AC于F,且AF=4cm,则AC的长为( )
 如图,BD=CD,AE:DE=1:2,延长BE交AC于F,且AF=4cm,则AC的长为( )
如图,BD=CD,AE:DE=1:2,延长BE交AC于F,且AF=4cm,则AC的长为( )| A. | 24cm | B. | 20cm | C. | 12cm | D. | 8cm |
 如图,已知△ABC内接于⊙O.半径为R,∠A为锐角.求证:$\frac{BC}{sinA}$=2R.
如图,已知△ABC内接于⊙O.半径为R,∠A为锐角.求证:$\frac{BC}{sinA}$=2R.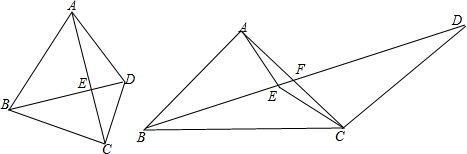
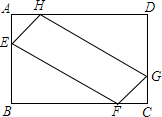 如图,在矩形ABCD中,AB=6,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且AE=AH=CF=CG,设AE的长为x,四边形EFGH的面积为S.
如图,在矩形ABCD中,AB=6,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且AE=AH=CF=CG,设AE的长为x,四边形EFGH的面积为S.