题目内容
16．
如图，已知△ABC内接于⊙O．半径为R，∠A为锐角．求证：$\frac{BC}{sinA}$=2R．
分析 连接CO并延长交⊙O于D，连接BD，根据圆周角定理得到∠D=∠A，∠DBC=90°，CD=2R，根据三角函数的定义即可得到结论．
解答 
证明：连接CO并延长交⊙O于D，连接BD，
∴∠D=∠A，∠DBC=90°，CD=2R，
在Rt△BCD中，sinD=$\frac{BC}{CD}$，
∴sinA=$\frac{BC}{2R}$．
点评 本题考查了圆周角定理，锐角三角函数，正确的作出辅助线是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
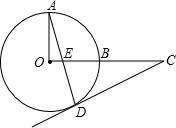如图，OA、OB是⊙O的两条半径，且OA⊥OB，点C是OB延长线上任意一点，过点C作CD切⊙O于点D，连接AD交OC于点E．求证：CD=CE．
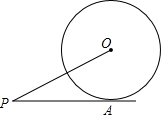如图，已知PA切⊙O于点A，OP=5，PA比⊙O的半径大1，求⊙O的半径．