题目内容
19.已知梯形ABCD的四个顶点的坐标分别为A(-2,0),B(6,0),C(2,2),D(0,2),直线y=kx+2将梯形分成面积相等的两部分,则k的值为$-\frac{2}{3}$.分析 直线y=kx+2经过D,求出梯形面积,然后求出直线与x轴的交点,即可求出k的值.
解答 解:直线y=kx+2恒过(0,2)即D点,
梯形的面积为:$\frac{(2+8)×2}{2}=10$,
直线y=kx+2与x轴的交点为E($-\frac{2}{k}$,0),
因为直线y=kx+2将梯形分成面积相等的两部分,
所以S△AED=$\frac{1}{2}×(-\frac{2}{k}+2)×2=5$,
所以k=$-\frac{2}{3}$.
故答案为:$-\frac{2}{3}$
点评 本题考查直线的交点,梯形的面积与三角形的面积公式的应用,直线系方程的利用,考查计算能力.

练习册系列答案
相关题目
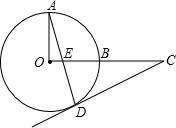 如图,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD交OC于点E.求证:CD=CE.
如图,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD交OC于点E.求证:CD=CE.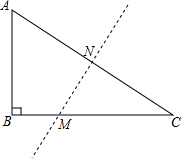 如图,在Rt△ABC中,∠B=90°,AC=10,AB=6,沿直线MN对折后,点C恰好与点A重合,试求MB的长.
如图,在Rt△ABC中,∠B=90°,AC=10,AB=6,沿直线MN对折后,点C恰好与点A重合,试求MB的长.