题目内容
2.已知抛物线y=x2-2mx+m2+m-4的顶点A在第四象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与点A、B重合),过点C作CD⊥x轴于点D,并交抛物线于点P.(1)求抛物线y=x2-2mx+m2+m-4顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围;
(2)若直线AP交y轴的负半轴于点E,且$\frac{CP}{AC}=1$,求△OEP的面积S的取值范围.
分析 (1)抛物线解析式为y=x2-2mx+m2+m-4,设顶点的坐标为(x,y),利用抛物线顶点坐标公式得到x=m,y=m-4,然后消去m得到y与x的关系式即可.
(2)如图,根据已知得出OE=4-2m,E(0,2m-4),设直线AE的解析式为y=kx+2m-4,代入A的坐标根据待定系数法求得解析式,然后联立方程求得交点P的坐标,根据三角形面积公式表示出S=$\frac{1}{2}$(4-2m)(m-1)=-m2+3m-2=-(m-$\frac{3}{2}$)2+$\frac{1}{4}$,即可得出S的取值范围.
解答 解:(1)由抛物线y=x2-2mx+m2+m-4可知,a=1,b=-2m,c=m2+m-4,
设顶点的坐标为(x,y),
∵x=-$\frac{b}{2}$=m,
∴b=-2m,
y=$\frac{4c-{b}^{2}}{4}$=$\frac{4({m}^{2}+m-4)-(-2m)^{2}}{4}$=m-4=x-4,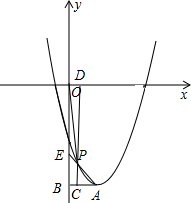
即顶点的纵坐标随横坐标变化的函数解析式为y=x-4(0<x<4);
(2)如图,由抛物线y=x2-2mx+m2+m-4可知顶点A(m,m-4),
∵$\frac{CP}{AC}=1$,
∴$\frac{BE}{AB}$=1,
∵AB=m,
∴BE=m,
∵OB=4-m,
∴OE=4-m-m=4-2m,
∴E(0,2m-4),
设直线AE的解析式为y=kx+2m-4,
代入A的坐标得,m-4=km+2m-4,解得k=-1,
∴直线AE的解析式为y=-x+2m-4,
解$\left\{\begin{array}{l}{y=-x+2m-4}\\{y={x}^{2}-2mx+{m}^{2}+m-4}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=m}\\{{y}_{2}=m-4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=m-1}\\{{y}_{2}=m-3}\end{array}\right.$,
∴P(m-1,m-3),
∴S=$\frac{1}{2}$(4-2m)(m-1)=-m2+3m-2=-(m-$\frac{3}{2}$)2+$\frac{1}{4}$,
∴S有最大值$\frac{1}{4}$,
∴△OEP的面积S的取值范围:0≤S≤$\frac{1}{4}$.
点评 本题考查了二次函数的性质以及抛物线的顶点坐标的求法,待定系数法求解析式,二次函数的最值等,本题的关键是记住抛物线的顶点坐标公式.

| A. | 0<m<1 | B. | -1<m<0 | C. | -2<m<-1 | D. | -3<m<-2 |
 如图,在△ABC中,DE是边AC的垂直平分线,AC=6cm,△ABD的周长为13cm,则△ABC的周长为19cm.
如图,在△ABC中,DE是边AC的垂直平分线,AC=6cm,△ABD的周长为13cm,则△ABC的周长为19cm. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于50°.
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于50°.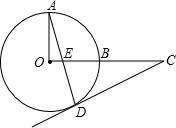 如图,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD交OC于点E.求证:CD=CE.
如图,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD交OC于点E.求证:CD=CE.