题目内容
1.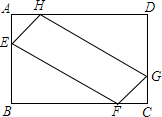 如图,在矩形ABCD中,AB=6,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且AE=AH=CF=CG,设AE的长为x,四边形EFGH的面积为S.
如图,在矩形ABCD中,AB=6,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且AE=AH=CF=CG,设AE的长为x,四边形EFGH的面积为S.(1)求S与x的函数表达式;
(2)当x为何值时,S的值最大?求出最大值.
分析 (1)利用四边形的面积等于矩形的面积减去四个直角三角形的面积,得到y与x的函数关系.
(2)通过对函数配方,求出函数的对称轴,对称轴在定义域内,在对称轴处取得最值.
解答 解:(1)因为△AEH≌△CFG,△EBF≌△HDG,
所以y=S矩形ABCD-2S△AEH-2S△EFB=6×8-2×$\frac{1}{2}$x2-2×$\frac{1}{2}$(8-x)(6-x)=-2x2+14x(0<x≤6).
(2)y=-2x2+3x=-2(x-$\frac{7}{2}$)2+$\frac{49}{2}$.
所以当x=$\frac{7}{2}$时,ymax=$\frac{49}{2}$.
点评 本题主要考查的是二次函数的应用,利用四边形的面积等于矩形的面积减去四个直角三角形的面积得到函数的关系式是解题的关键.

练习册系列答案
相关题目
16.2012年某事摩托车全年排放有害污染物一览表:
材料二:2012年元月10日,南宁市人民政府下达了停止办理摩托车入户手续文件,此时市区居民摩托车拥有、量已达32万辆.据统计每7辆摩托车排放的有害污染物总量等于一辆公交车排放的污染物,而每辆摩托车的运送能力是一辆公交车运送能力的8%.
(1)根据上表填空:I、2000年南宁市区机动车(含摩托车)全年排放的有害污染物共3.2×104吨
(2)假设从2002年起,2年内南宁市的摩托车平均每年退役a万辆,同时增加公交车的数量,使新增公交车的运送能力总量等于退役的摩托车原有的运送能力总量.
①试找出增加公交车的数量y与时间n(年)之间的函数关系.
②若经过5年剩余的摩托车与新增公交车排放污染物的总量等于32万辆摩托车排放污染物总量的34%.求a的值.
| 有害污染物 | 排放量 | 占市区道路行驶机动车(含摩托车) 排放有害污染物总量 |
| 一氧化碳 | 11342吨 | 50% |
| 氮氧化物 | 2380吨 | |
| 非甲烷烃 | 2044吨 |
(1)根据上表填空:I、2000年南宁市区机动车(含摩托车)全年排放的有害污染物共3.2×104吨
(2)假设从2002年起,2年内南宁市的摩托车平均每年退役a万辆,同时增加公交车的数量,使新增公交车的运送能力总量等于退役的摩托车原有的运送能力总量.
①试找出增加公交车的数量y与时间n(年)之间的函数关系.
②若经过5年剩余的摩托车与新增公交车排放污染物的总量等于32万辆摩托车排放污染物总量的34%.求a的值.
10.下列方程为一元一次方程的是( )
| A. | 2x-3=y | B. | x2-2x-3=0 | C. | x=0 | D. | $\frac{1}{y}$-1=y |
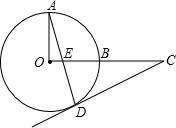 如图,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD交OC于点E.求证:CD=CE.
如图,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD交OC于点E.求证:CD=CE.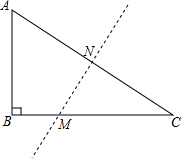 如图,在Rt△ABC中,∠B=90°,AC=10,AB=6,沿直线MN对折后,点C恰好与点A重合,试求MB的长.
如图,在Rt△ABC中,∠B=90°,AC=10,AB=6,沿直线MN对折后,点C恰好与点A重合,试求MB的长.