题目内容
6.已知△ABC纸片(1)如图甲,将△ABC纸片折叠,使C落在三角形的内部,求证:∠ADC+∠BEC=2∠C;
(2)如图乙,将△ABC纸片折叠,使C落在三角形的外部,(1)中的结论还成立吗?若不成立,直接写出∠ADC、∠BEC、∠C之间的数量关系.
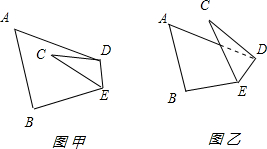
分析 (1)首先根据四边形内角和定理可得:∠ADC+∠BEC+(180°-∠C)+∠A+∠B=360°,整理可得结论;
(2)利用四边形的内角和定理和三角形的内角和定理可得∠BEC+∠CED+∠ADE=180°+∠C,再利用三角形的内角和定理可得∠CED+∠ADE=180°-∠C-∠ADC,再代入整理即可得出结论.
解答 (1)证明:∵∠ADC+∠BEC+(180°-∠C)+∠A+∠B=360°
∴∠ADC+∠BEC=360°-(180°-∠C)-∠A-∠B=180°-∠A-∠B+∠C=2∠C;
(2)解:∠BEC-∠ADC=2∠C.
∵∠BEC+∠CED+∠ADE=360°-(∠A+∠B),∠A+∠B=180°-∠C,
∴∠BEC+∠CED+∠ADE=180°+∠C,
∵∠CED+∠ADE+∠ADC=180°-∠C,
∴∠CED+∠ADE=180°-∠C-∠ADC,
∴∠BEC+(180°-∠C-∠ADC)=180°+∠C,
∴∠BEC-∠ADC=2∠C.
点评 该题主要考查了翻折变换的性质、三角形内角和定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、三角形内角和定理来分析、判断、推理或解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.如图(1),在矩形ABCD中,动点P从点B出发,沿着BC、CD、DA运动到点A停止,设点P运动的路程为x,△ABP的面积为y,如果y与x的函数图象如图(2)所示,则△ABC的周长为( )
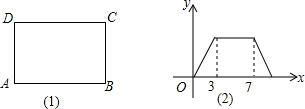

| A. | 9 | B. | 6 | C. | 12 | D. | 7 |
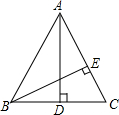 如图,在△ABC中,AD是BC边上的高线,BE⊥AC于点E,∠BAD=∠CBE.
如图,在△ABC中,AD是BC边上的高线,BE⊥AC于点E,∠BAD=∠CBE.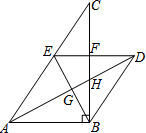 如图,在△ABC中,∠ABC=90°,过点B作AC的平行线交∠CAB的平分线于点D,过点D作AB的平行线交AC于点E,交BC于点F,连接BE,交AD于点G.
如图,在△ABC中,∠ABC=90°,过点B作AC的平行线交∠CAB的平分线于点D,过点D作AB的平行线交AC于点E,交BC于点F,连接BE,交AD于点G.




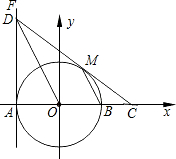 如图,在平面直角坐标系xOy中,⊙O交x轴于A,B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.
如图,在平面直角坐标系xOy中,⊙O交x轴于A,B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C. 如图,直角梯形ABCD中,∠BAD=90°,AC⊥BD,已知BC:AD=k.求AC:BD的值.
如图,直角梯形ABCD中,∠BAD=90°,AC⊥BD,已知BC:AD=k.求AC:BD的值.