题目内容
2.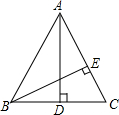 如图,在△ABC中,AD是BC边上的高线,BE⊥AC于点E,∠BAD=∠CBE.
如图,在△ABC中,AD是BC边上的高线,BE⊥AC于点E,∠BAD=∠CBE.求证:AB=AC.
分析 根据三角形的内角和得到∠ABC+∠BAD=∠C+∠CBE=90°,由等式的性质得到∠ABC=∠C,根据等腰三角形的判定定理即可得到结论.
解答 证明:∵AD是BC边上的高线,BE⊥AC于点E,
∴∠ADB=∠BEC=90°,
∴∠ABC+∠BAD=∠C+∠CBE=90°,
∵∠BAD=∠CBE,
∴∠ABC=∠C,
∴AB=AC.
点评 本题考查了等腰三角形的判定定理,直角三角形的性质,熟记等腰三角形的判定是解题的关键.

练习册系列答案
相关题目
14.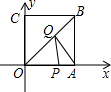 如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点P在OA上,且P点的坐标为(3,0),Q是OB上一动点,则PQ+AQ的最小值为( )
如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点P在OA上,且P点的坐标为(3,0),Q是OB上一动点,则PQ+AQ的最小值为( )
 如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点P在OA上,且P点的坐标为(3,0),Q是OB上一动点,则PQ+AQ的最小值为( )
如图所示,四边形OABC是正方形,边长为4,点A、C分别在x轴、y轴的正半轴上,点P在OA上,且P点的坐标为(3,0),Q是OB上一动点,则PQ+AQ的最小值为( )| A. | 5 | B. | $\sqrt{10}$ | C. | 4 | D. | 6 |
7.若a=$\sqrt{2}$,b=$\sqrt{7}$-$\sqrt{3}$,c=$\sqrt{6}$-$\sqrt{2}$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | b<a<c |
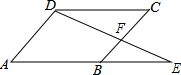 如图,E是?ABCD边AB延长线上的一点,AE=4BE,连接DE交BC于F,则$\frac{BF}{FC}$=$\frac{1}{3}$.
如图,E是?ABCD边AB延长线上的一点,AE=4BE,连接DE交BC于F,则$\frac{BF}{FC}$=$\frac{1}{3}$.
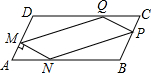 在一块?ABCD的空地上,划一块?MNPQ进行绿化,如图?MNPQ的顶点在?ABCD的边上,已知∠A=60°,∠AMN=90°,且AM=PC=xm,已知?ABCD的边BC=20m,AB=am,a为大于20m的常数,设四边形MNPQ的面积为Sm2.
在一块?ABCD的空地上,划一块?MNPQ进行绿化,如图?MNPQ的顶点在?ABCD的边上,已知∠A=60°,∠AMN=90°,且AM=PC=xm,已知?ABCD的边BC=20m,AB=am,a为大于20m的常数,设四边形MNPQ的面积为Sm2. 如图,平行四边形ABCD,AD=5,AB=6,点A的坐标为(-3,0),则点C的坐标为(6,4).
如图,平行四边形ABCD,AD=5,AB=6,点A的坐标为(-3,0),则点C的坐标为(6,4).