Question

15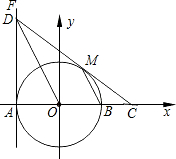．如图，在平面直角坐标系xOy中，⊙O交x轴于A，B两点，直线FA⊥x轴于点A，点D在FA上，且DO平行⊙O的弦MB，连DM并延长交x轴于点C．
（1）判断直线DC与⊙O的位置关系，并证明；
（2）设点D的坐标为（-6，12），C的坐标为（10，0），试求MC的长．

Answer 1

分析 （1）通过证明三角形AOD和DOM全等来求解．已知的条件有OA=OM，一条公共边OD，只要证明出两组对应边的夹角相等即可，可通过OD∥MB，OM=OB来证OM⊥DC，得出答案即可．
（2）求MC的长就要求出DC的长，由D的坐标以及C点坐标，可得AD，OA，AC的长，进而利用勾股定理求出答案．

解答 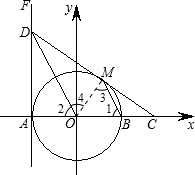解：（1）直线DC与⊙O相切于点M．
理由如下：如图所示：连接OM，
∵DO∥MB，
∴∠1=∠2，∠3=∠4．
∵OB=OM，
∴∠1=∠3．
∴∠2=∠4．
在△DAO与△DMO中，
$\left\{\begin{array}{l}{AO=OM}\\{∠2=∠4}\\{DO=DO}\end{array}\right.$，
∴△DAO≌△DMO（SAS）．
∴∠OMD=∠OAD．
由于FA⊥x轴于点A，
∴∠OAD=90°．
∴∠OMD=90°．即OM⊥DC．
∴DC切⊙O于M．

（2）由点D的坐标为（-6，12），知OA=6（即⊙O的半径），AD=12．
由（1）知DM=AD=12，由△OMC∽△DAC，知$\frac{MC}{AC}$=$\frac{OM}{AD}$=$\frac{6}{12}$=$\frac{1}{2}$．
∴AC=2MC，
在Rt△ACD中，CD=MC+12．
由勾股定理，有（6+10）²+12²=（MC+12）²，
解得：MC=8，．
∴MC的长为8．

点评 本题综合考查了全等三角形，相似三角形的判断与性质，利用全等三角形和相似三角形来得出线段相等或成比例是解题的关键．