题目内容
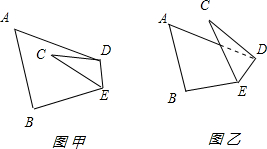
16. 如图,直角梯形ABCD中,∠BAD=90°,AC⊥BD,已知BC:AD=k.求AC:BD的值.
如图,直角梯形ABCD中,∠BAD=90°,AC⊥BD,已知BC:AD=k.求AC:BD的值.
分析 根据题意,得Rt△ABC∽Rt△DBA,得出两个比例式,两式相乘,即得结论.
解答 解:∵直角梯形ABCD中,∠A=90°,AC⊥BD,
∴∠BAD=∠CBA=90°,∠ACB+∠DBC=90°,∠ABD+∠DBC=90°,
∴∠ACB=∠ABD,
∴Rt△ABC∽Rt△DAB,
∴$\frac{AC}{BD}$=$\frac{BC}{AB}$ ①,$\frac{AC}{BD}$=$\frac{AB}{AD}$ ②,
①×②得$\frac{A{C}^{2}}{B{D}^{2}}$=$\frac{BC}{AD}$.
即$\frac{AC}{BD}$=$\sqrt{k}$.
点评 本题考查了相似三角形的判定和性质,根据已知线段的比与待求线段的比知待证相似三角形是解题的切入点,熟练应用相似三角形的性质对比例式灵活变形是解题的关键.

练习册系列答案
相关题目
7.若a=$\sqrt{2}$,b=$\sqrt{7}$-$\sqrt{3}$,c=$\sqrt{6}$-$\sqrt{2}$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | b<a<c |
 Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线$y=\frac{k}{x}(k≠0)$经过CD点及AB的中点D,S△BCD=4,则k的值为( )
Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线$y=\frac{k}{x}(k≠0)$经过CD点及AB的中点D,S△BCD=4,则k的值为( )