题目内容
16.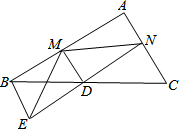 如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.(1)求证:BE=CN;
(2)试判断BM+CN与MN的大小关系,并说明理由.
分析 (1)先利用ASA判定△BED≌△CND,从而得出BE=CN;
(2)再利用全等的性质可得ED=ND,再有DM⊥EN,从而得出ME=MN,两边和大于第三边从而得出BM+CN>MN.
解答 (1)证明:∵BE∥AC,
∴∠DBE=∠DCN,
∵D为BC的中点,
∴BD=CD,
在△BED与△CND中,$\left\{\begin{array}{l}{∠DBE=∠DCN}\\{BD=CD}\\{∠BDE=∠CDN}\end{array}\right.$,
∴△BED≌△CND(ASA),
∴BE=CN;
(2)解:BM+CN>MN.
∵△BED≌△CND,
∴ED=ND,BE=CN.
又∵DM⊥NE,
∴ME=MN(垂直平分线到线段端点的距离相等).
∴在△MBE中,BM+BE>ME,
即BM+CN>MN.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
1.下列图形中,既是轴对称图形又是中心对称图形的是:( )
| A. |  | B. |  | C. |  | D. |  |
 如图,抛物线y=-x2+bx+c与直线AB相交于A(-1,0)、B(2,3)两点,与y轴交于点C,其顶点为D.
如图,抛物线y=-x2+bx+c与直线AB相交于A(-1,0)、B(2,3)两点,与y轴交于点C,其顶点为D.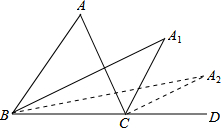 如图,已知△ABC的内角∠A=α°,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2014,则∠A2014的度数是$\frac{1}{{2}^{2014}}$α.
如图,已知△ABC的内角∠A=α°,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2014,则∠A2014的度数是$\frac{1}{{2}^{2014}}$α.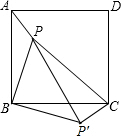 如图,点P是正方形ABCD内的一点,连接AP,BP,CP.将△PAB绕着点B顺时针旋转90°到△P′CB的位置,若AP=2,BP=4,∠APB=135°.求PP′及PC的长.
如图,点P是正方形ABCD内的一点,连接AP,BP,CP.将△PAB绕着点B顺时针旋转90°到△P′CB的位置,若AP=2,BP=4,∠APB=135°.求PP′及PC的长.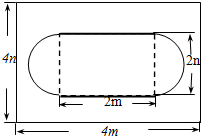 某居民小区为了美化环境,如图在一块长为4m,宽为4n的长方形绿地上建造花坛,花坛是由一个矩形和两个半圆组成的.求改造后剩下的绿地面积(π取3).
某居民小区为了美化环境,如图在一块长为4m,宽为4n的长方形绿地上建造花坛,花坛是由一个矩形和两个半圆组成的.求改造后剩下的绿地面积(π取3).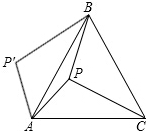 如图,P是等边△ABC内的一点,且PA=6,PB=8,若将△PAC绕点A逆时针旋转后,得到△P′AB,且∠APB=150°,则点P到P′之间的距离为6,PC=10.
如图,P是等边△ABC内的一点,且PA=6,PB=8,若将△PAC绕点A逆时针旋转后,得到△P′AB,且∠APB=150°,则点P到P′之间的距离为6,PC=10.