题目内容
11.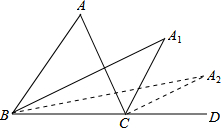 如图,已知△ABC的内角∠A=α°,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2014,则∠A2014的度数是$\frac{1}{{2}^{2014}}$α.
如图,已知△ABC的内角∠A=α°,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2014,则∠A2014的度数是$\frac{1}{{2}^{2014}}$α.
分析 由三角形的外角性质知:∠A=∠ACD-∠ABC,而∠A1=$\frac{1}{2}$(∠ACD-∠ABC),即∠A1=$\frac{1}{2}$∠A,同理可得,∠A2=$\frac{1}{2}$∠A1,依此类推即可.
解答 解:△ABC中,∵∠A=∠ACD-∠ABC,A1是∠ABC角平分与∠ACD的平分线的交点,∠A=α,
∴∠A1=∠A1CD-∠A1BC=$\frac{1}{2}$(∠ACD-∠ABC)=$\frac{1}{2}$∠A;
同理可得,∠A2=$\frac{1}{2}$∠A1=$\frac{1}{{2}^{2}}$∠A,
∠A3=$\frac{1}{2}$∠A2=$\frac{1}{{2}^{3}}$∠A,
…
依此类推,∠An=$\frac{1}{{2}^{n}}$∠A,即∠An=$\frac{α}{{2}^{n}}$.
∴∠A2014=$\frac{1}{{2}^{2014}}$α,
故答案为:$\frac{1}{{2}^{2014}}$α.
点评 本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形的内角和是180°是解答此题的关键.

练习册系列答案
相关题目
6. 如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )
如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )
 如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )
如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
16.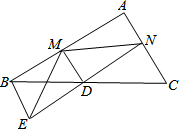 如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
(1)求证:BE=CN;
(2)试判断BM+CN与MN的大小关系,并说明理由.
 如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
如图,已知D是△ABC中一边BC上的中点,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.(1)求证:BE=CN;
(2)试判断BM+CN与MN的大小关系,并说明理由.
3.在平面直角坐标系中,抛物线y=x2+2x-3与x轴的交点个数是( )
| A. | 0个 | B. | 1 个 | C. | 2个 | D. | 3个 |
20.下列方程中,是二元一次方程的为( )
| A. | $x-\frac{1}{x}=3$ | B. | x+xy=-1 | C. | $\frac{x}{3}-\frac{y}{5}=6$ | D. | x2-2x-1=0 |
1.下列运算中正确的是( )
| A. | a3+a4=a12 | B. | 2(a+1)=2a+1 | C. | (-2a3)2=8a5 | D. | (3a2-a3)•a=3a3-a4 |
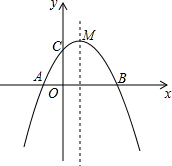 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=OC,M是抛物线的顶点,三角形AMB的面积等于1,则下列结论:
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=OC,M是抛物线的顶点,三角形AMB的面积等于1,则下列结论: 将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.
将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.